0, for all practical purposes,
see also Zero-based indexing
o (composition)
o (composition)
 (``chart'' function)
(``chart'' function)
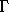 [q]
[q]
for local tuple
Lagrangian state path
 L[q] (Hamiltonian state path)
L[q] (Hamiltonian state path)
 (coordinate function)
(coordinate function)
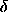 function
function
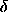
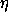 (variation operator)
(variation operator)
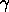 (configuration-path function)
(configuration-path function)
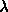 -calculus
-calculus
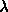 -expression
-expression
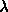 -notation
-notation
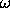 matrix
matrix
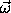 (angular velocity)
(angular velocity)
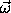 (t) × operator
(t) × operator
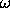 (symplectic 2-form)
(symplectic 2-form)
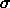 (phase-space path)
(phase-space path)
A
C (canonical phase-space transformation)
C (local-tuple transformation)
D, see Derivative
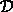 vs. D
vs. D
 , see Partial derivative
, see Partial derivative
Dt (total time derivative)
E (Euler-Lagrange operator)
 (energy state function)
(energy state function)
F1-F4, see also Generating functions
F1(t, q, q')
F2(t, q, p')
F3(t, p, q')
F4(t, p, p')
H (Hamiltonian)
Ii, Iz (selector),
[2]
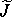 (shuffle function)
(shuffle function)
J, Jn (symplectic unit), [2]
L (Lie derivative)
L or L (Lagrangian)
(Lagrangian)
vs. 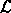
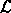 (Lagrangian)
(Lagrangian)
P (momentum selector),
[2]
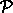 (momentum state function)
(momentum state function)
Q (coordinate selector)
q (coordinate path)
S or S (action)
(action)
vs. 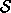
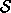 (action)
(action)
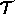 [
[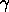 ]
]
' (quote in Scheme)
, in tuple
:, names starting with
; in tuple, [2]
# in Scheme
{ } for Poisson brackets
[ ] for down tuples
[ ] for functional arguments
( ) for up tuples
() in Scheme,
[2], [3]
A
Action
computing
coordinate representation of
coordinate-independence of,
[2]
free particle
generating functions and
Hamilton-Jacobi equation and
Lagrangian
minimizing
parametric
principles, see Principle of stationary action
S or S
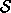
time evolution and,
[2]
variation of
Action principle, see Principle of stationary action
Action-angle coordinates
Hamilton's equations in
Hamilton-Jacobi equation and
Hamiltonian in
harmonic oscillator in
perturbation of Hamiltonian,
[2]
surfaces of section in
Action-like region
Alphabet, insufficient size of
Alternative in conditional
Angles, Euler, see Euler angles
Angular momentum, see also Vector angular momentum
conservation of,
[2], [3],
[4]
equilibrium points for
Euler's equations and
kinetic energy in terms of
Lie commutation relations for
as Lie generator of rotations
of free rigid body,
[2]
of rigid body
sphere of
z component of
Angular velocity vector (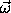 ), [2]
), [2]
Euler's equations for
kinetic energy in terms of,
[2]
representation of
Anomaly, true
antisymmetric->column-matrix
Antisymmetry of Poisson bracket
Area preservation
by maps
Liouville's theorem and
Poincaré-Cartan integral invariant and
of surfaces of section,
[2]
Arguments
active vs. passive in Legendre transformation
in Scheme
Arithmetic
generic, [2],
[3]
on functions,
[2]
on operators,
[2]
on procedures
on symbolic values
on tuples, [2]
Arnold, V. I., [2],
[3],
see also Kolmogorov-Arnold-Moser theorem
Associativity and non-associativity of tuple multiplication, [2]
Asteroids, rotational alignment of
Astronomy, see Celestial objects
Asymptotic trajectories,
[2], [3]
Atomic scale
Attractor
Autonomous systems,
see also Extended phase space
surfaces of section for
Awake top
Axes, principal
of this dense book
Axisymmetric potential of galaxy
Axisymmetric top
awake
behavior of,
[2]
conserved quantities for
degrees of freedom of
Euler angles for
Hamiltonian treatment of
Lagrangian treatment of
nutation of
potential energy for
precession of,
[2]
rotation of
sleeping
symmetries of
Baker, Henry, see Baker-Campbell-Hausdorff formula
Baker-Campbell-Hausdorff formula
Banana, see Book
Barrow-Green, June
Basin of attraction
Bicycle wheel
Birkhoff, George David, see Poincaré-Birkhoff theorem
bisect (bisection search),
[2]
Body components of vector
Boltzmann, Ludwig,
[2], [3]
Book
banana-like behavior of
rotation of,
[2]
Brackets, see also Poisson brackets
for down tuples
for functional arguments
Bulirsch-Stoer integration method
bulirsch-stoer
Butterfly effect
C (canonical phase-space transformation)
C (local-tuple transformation)
Campbell, John, see Baker-Campbell-Hausdorff formula
Canonical equations, see Hamilton's equations
Canonical heliocentric coordinates
Canonical perturbation theory, see Perturbation theory
Canonical plane
Canonical transformations,
see also Generating functions; Symplectic transformations
classical gauge
composition of,
[2], [3]
conditions for
for driven pendulum
general
group properties of
for harmonic oscillator
invariance of antisymmetric bilinear form under
invariance of phase volume under
invariance of Poisson brackets under
invariants of,
see also Integral invariants
as Lie series
Lie transforms, see Lie transforms
point transformations, see Point transformations
polar-canonical, see Polar-canonical transformation
to rotating coordinates,
[2]
symplectic-matrix test
time evolution as
time-dependent
time-independent
canonical?
Cantori, [2]
car
Cartan, Élie, see Poincaré-Cartan integral invariant
Cauchy, Augustin Louis
cdr
Celestial objects, see also Asteroids; Comets; Earth; Galaxy; Hyperion; Jupiter; Mercury; Moon; Phobos; Planets
rotation of,
[2], [3]
Center of mass
in two-body problem
Jacobi coordinates and
kinetic energy and
vector angular momentum and
Central force
collapsing orbits
epicyclic motion
gravitational
in 2 dimensions,
[2], [3]
in 3 dimensions
Lie series for motion in
reduced phase space for motion in
Central potential, see Central force
Chain rule
for derivatives,
[2]
for partial derivatives,
[2]
for total time derivatives
in traditional notation
for variations
Chaotic motion,
see also Exponential divergence
homoclinic tangle and
in Hénon-Heiles problem
in spin-orbit coupling,
[2]
near separatrices,
[2], [3]
of Hyperion,
[2]
of non-axisymmetric top
of periodically driven pendulum,
[2]
overlapping resonances and
Characteristic exponent
Characteristic multiplier
Chart function (
 )
)
Chirikov, Boris V.
Chirikov-Taylor map
Church, Alonzo
Classical gauge transformations
Colon, names starting with
Comets, rotation of
Comma in tuple
Commensurability,
see also Resonance
islands and
of pendulum period with drive,
[2]
periodic orbits and,
[2]
rational rotation number and
small denominators and
Commutativity, see also Non-commutativity
of some tuple multiplication
of variation (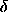 ) with differentiation and integration
) with differentiation and integration
Commutator
of angular-momentum Lie operators
Jacobi identity for
of Lie derivative
Poisson brackets and
Compatible shape
compatible-shape
component, [2]
compose
Composition
of canonical transformations,
[2], [3]
of functions,
[2], [3]
of Lie transforms
of linear transformations
of operators
of rotations
Compositional canonical
compositional-canonical?
Compound data in Scheme
cond
Conditionals in Scheme
Configuration
Configuration manifold
Configuration path, see Path
Configuration space
Configuration-path function (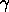 ),
[2]
),
[2]
Conjugate momentum
non-uniqueness of
cons
Consequent in conditional
Conserved quantities,
[2],
see also Hénon-Heiles problem, integrals of motion
angular momentum,
[2], [3],
[4]
coordinate choice and
cyclic coordinates and
energy, [2],
[3]
Jacobi constant
Lyapunov exponents and
momentum
Noether's theorem
phase space reduction and
phase volume, see Phase-volume conservation
Poisson brackets of
symmetry and, [2]
for top
Constant of motion (integral of motion),
see also Conserved quantities; Hénon-Heiles problem
Constraint force
Constraint(s)
augmented Lagrangian and,
[2]
configuration space and
as coordinate transformations
explicit
in extended bodies
holonomic, [2]
integrable, [2]
linear in velocities
nonholonomic (non-integrable)
on coordinates
rigid
as subsystem couplers
total time derivative and
velocity-dependent
velocity-independent
Constructors in Scheme
Contact transformation, see Canonical transformations
Continuation procedure
Continued-fraction approximation of irrational number
Contraction of tuples
coordinate
Coordinate function ( )
)
Coordinate path (q),
see also Local tuple
Coordinate singularity
Coordinate transformations
constraints as
Coordinate(s), see also Generalized coordinates
action-angle, see Action-angle coordinates
conserved quantities and choice of
constraints on
cyclic, [2]
heliocentric
ignorable (cyclic)
Jacobi
polar, see Polar coordinates
redundant, and initial conditions
rotating, see Rotating coordinates
spherical
Coordinate-independence
of action, [2]
of Lagrange equations,
[2]
of variational formulation,
[2]
Correction fluid
Cotangent space, bundle
Coupling systems
Coupling, spin-orbit, see Spin-orbit coupling
Curves, invariant, see Invariant curves
Cyclic coordinate,
[2]
D, see Derivative
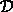 vs. D
vs. D
D (Scheme procedure for derivative), [2]
 , see Partial derivative
, see Partial derivative
Dt (total time derivative)
d'Alembert-Lagrange principle (Jean leRond d'Alembert)
Damped harmonic oscillator
define
Definite integral
definite-integral
Definitions in Scheme
Degrees of freedom
Delta function
Derivative, [2],
see also Total time derivative
as operator
as Poisson bracket
chain rule, [2]
in Scheme programs: D,
[2]
notation: D,
[2]
of function of multiple arguments,
[2]
of function with structured arguments
of function with structured inputs and outputs
of state
partial, see Partial derivative
precedence of,
[2]
with respect to a tuple
determinant
Differentiable manifold
Dimension of configuration space
Dirac, Paul Adrien Maurice
Dissipation of energy
in free-body rotation
tidal friction
Dissipative system, phase-volume conservation
Dissolution of invariant curves,
[2]
Distribution functions
Divided phase space,
[2], [3]
Division in Scmutils
by a structure
generic character of
of vector by matrix
Dot notation
down, [2]
Down tuples
Driven harmonic oscillator
Driven pendulum, see Pendulum (driven)
Driven rotor, [2]
Dt (total time derivative)
Dynamical state, see State
E (Euler-Lagrange operator)
 (energy state function)
(energy state function)
Earth
precession of
rotational alignment of
Effective Hamiltonian
Eigenvalues and eigenvectors
for equilibria
for fixed points
for Hamiltonian systems
of inertia tensor
for unstable fixed point
Einstein summation convention
Einstein, Albert
else
Empty list
Energy
as sum of kinetic and potential energies
conservation of,
[2], [3]
dissipation of, see Dissipation of energy
Energy state function ( )
)
Hamiltonian and
Epicyclic motion
eq?
Equilibria, [2],
[3], see also Fixed points
for angular momentum
inverted, for pendulum,
[2], [3],
[4]
linear stability of
relative
stable and unstable
Equinox, precession of
Ergodic motion
Ergodic theorem
Euler, Leonhard
Euler angles
for axisymmetric top
kinetic energy in terms of
singularities and,
[2]
Euler-Lagrange-operator ( E )
Euler's equations
singularities in
Euler's theorem on homogeneous functions
Euler's theorem on rotations
Euler angles and
Euler-Lagrange equations, see Lagrange equations
Euler-Lagrange operator ( E )
Euler->M
Euler-state->L-space
Euler-state->omega-body
Evolution, see Time evolution of state
evolve, [2],
[3]
explore-map
Exponential divergence,
[2], [3],
see also Lyapunov exponent
homoclinic tangle and
Exponential(s)
of differential operator
of Lie derivative
of noncommuting operators
Expressions in Scheme
Extended phase space
generating functions in
F1-F4, see also Generating functions
F1(t, q, q')
F2(t, q, p')
F3(t, p, q')
F4(t, p, p')
F->C, [2]
F->CT
Fermat, Pierre, [2]
Fermat's principle (optics),
[2]
Fermi, Enrico
Feynman, Richard P.
find-path
First amendment, see Degrees of freedom
First integral
Fixed points,
see also Equilibria
elliptic, [2]
equilibria or periodic motion and,
[2]
for Hamiltonian systems
hyperbolic, [2]
linear stability of
manifolds for
parabolic
Poincaré-Birkhoff fixed points
Poincaré-Birkhoff theorem
rational rotation number and
Floating-point numbers in Scheme
Floquet multiplier
Flow, defined by vector field
Force
central, see Central force
exerted by constraint
Forced libration of the Moon
Forced rigid body, see Rigid body, forced
Formal parameters
of a function
of a procedure
frame
Free libration of the Moon
Free particle
action
Lagrange equations for
Lagrangian for
Free rigid body, see Rigid body (free)
Freudenthal, Hans
Friction
internal
tidal
Function definition
Function(s)
arithmetic operations on,
[2]
composition of,
[2], [3]
homogeneous
operators vs.,
[2]
orthogonal, tuple-valued
parallel, tuple-valued
selector, [2]
tuple of, [2]
vs. value when applied,
[2]
with multiple arguments,
[2], [3]
with structured arguments,
[2], [3]
with structured output,
[2]
Functional arguments
Functional mathematical notation,
[2]
Fundamental Poisson brackets
Galaxy
axisymmetric potential of
Gamma (Scheme procedure for 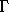 )
)
optional argument
Gamma-bar
Gas in corner of room
Gauge transformations, classical
Generalized coordinates,
[2], [3]
Euler angles as,
see also Euler angles
Lagrangian in
Generalized momentum
transformation of
Generalized velocity
transformation of
Generating functions
classical gauge transformations and
in extended phase space
F1-F4
F1
F2
F2 and point transformations
F2 for polar coordinate transformation
F2 for rotating coordinates
incorrect derivation of
integral invariants and
Lagrangian action and
Legendre transformation between F1 and F2
Generic arithmetic,
[2], [3]
Gibbs, Josiah Willard,
[2]
Golden number
Golden ratio, a most irrational number
Golden rotation number
Goldstein, Herbert
Goldstein's hoop
Golf ball, tiny
Grand Old Duke of York, see neither up nor down
Graphing, [2],
[3]
Gravitational potential
central
of galaxy
multipole expansion of
rigid-body
Group properties
of canonical transformations
of rotations, see Euler's theorem on rotations
H (Hamiltonian)
H-central
H-harmonic
H-pend-sysder
Hamilton, Sir William Rowan,
[2]
Hamilton's equations
in action-angle variables
computation of
dynamical
for central potential
for damped harmonic oscillator
for harmonic oscillator
from action principle
from Legendre transformation
numerical integration of
Poisson bracket form
Hamilton's principal function 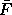
Hamilton's principle
for systems with rigid constraints
Hamilton-Jacobi equation
action at endpoints and
action-angle coordinates and
for harmonic oscillator
for Kepler problem
separation in spherical coordinates
time-independent
Hamiltonian
in action-angle variables
computing, see H-...
cyclic in coordinate
energy state function and
for axisymmetric potential
for central potential,
[2], [3],
[4]
for damped harmonic oscillator
for driven pendulum,
[2]
for driven rotor
for harmonic oscillator
for harmonic oscillator, in action-angle coordinates
for Kepler problem
for pendulum
for periodically driven pendulum,
[2]
for restricted three-body problem,
[2]
for top
for two-body problem
Hénon-Heiles,
[2]
Lagrangian and,
[2]
perturbation of action-angle,
[2]
time-dependent, and dissipation
Hamiltonian flow
Hamiltonian formulation
Lagrangian formulation and
Hamiltonian state
Hamiltonian state derivative,
[2]
Hamiltonian state path  L[q]
L[q]
Hamiltonian->Lagrangian
Hamilton-equations
Harmonic oscillator
coupled
damped
decoupling via Lie transform
driven
first-order equations for
Hamilton's equations for
Hamiltonian for
Hamiltonian in action-angle coordinates
Lagrange equations for,
[2]
Lagrangian for
Lie series for
solution of, [2]
solution via canonical transformation
solution via Hamilton-Jacobi
Hausdorff, Felix, see Baker-Campbell-Hausdorff formula
Heiles, Carl, [2],
see also Hénon
Heisenberg, Werner,
[2]
Heliocentric coordinates
Hénon, Michel, [2],
[3]
Hénon-Heiles problem
computing surfaces of section
history of
integrals of motion,
[2], [3]
interpretation of model
model of
potential energy
surface of section
Hénon's quadratic map
Heteroclinic intersection
Higher-order perturbation theory,
[2]
History
Hénon-Heiles problem
variational principles,
[2], [3],
[4]
Holonomic system, [2]
Homoclinic intersection
Homoclinic tangle
chaotic regions and
computing
exponential divergence and
Homogeneous function, Euler's theorem
Huygens, Christiaan
Hyperion, chaotic tumbling of,
[2]
Ii, Iz (selector),
[2]
if
Ignorable coordinate, see Cyclic coordinate
Indexing, zero-based, see Zero-based indexing
Inertia matrix,
see also Inertia tensor
Inertia tensor
diagonalization of
kinetic energy in terms of
principal axes of
transformation of
Inertia, moments of, see Moment(s) of inertia
Initial conditions, see Sensitivity to initial conditions; State
Inner product of tuples
Instability, see also Equilibria; Linear stability
free-body rotation
Integers in Scheme
Integrable constraints,
[2]
Integrable systems
periodic orbits of near-integrable systems
perturbation of,
[2], [3]
reduction to quadrature and,
see also Quadrature
surfaces of section for
Integral invariants
generating functions and
Poincaré
Poincaré-Cartan,
[2]
Integral of motion,
see also Conserved quantities; Hénon-Heiles problem
Integral, definite
Integration, see Numerical integration
Invariant curves,
[2]
dissolution of,
[2]
finding (computing)
finding (strategy)
irrational rotation number and
Kolmogorov-Arnold-Moser theorem
Invariants of canonical transformations,
see also Integral invariants
Irrational number, continued-fraction approximation
Islands in surfaces of section, see also Resonance
for Hénon-Heiles problem
for periodically driven pendulum,
[2], [3]
for standard map
perturbative vs. actual
in Poincaré-Birkhoff construction
Poisson series and
secondary, [2]
size of, [2]
small denominators and,
[2]
Iteration in Scheme
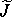 (shuffle function)
(shuffle function)
J, Jn (symplectic unit), [2]
J-func (shuffle function)
Jac (Jacobian of map)
Jacobi constant
Jacobi coordinates
Jacobi identity
for commutators
for Poisson brackets
Jacobi, Carl Gustav Jacob,
see also Hamilton-Jacobi equation
Jacobian
Jeans, Sir James, ``theorem'' of
Jupiter
KAM theorem, see Kolmogorov-Arnold-Moser theorem
Kepler problem
in reduced phase space
solution via Hamilton-Jacobi equation
Kepler's third law
Kepler, Johannes, see Kepler...
Kinematics of rotation
Kinetic energy
ellipsoid of
in Lagrangian
as Lagrangian for free body
as Lagrangian for free particle
of axisymmetric top
of free rigid body
of rigid body,
see also Rigid body, kinetic energy...
rotational and translational
in spherical coordinates
Knuth, Donald E.
Kolmogorov, A. N., see Kolmogorov-Arnold-Moser theorem
Kolmogorov-Arnold-Moser theorem,
[2]
L (Lie derivative)
L or L (Lagrangian)
(Lagrangian)
vs. 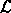
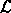 (Lagrangian)
(Lagrangian)
L-axisymmetric-top
L-central-polar,
[2]
L-central-rectangular
L-free-particle
L-harmonic
L-pend
L-rectangular
L-uniform-acceleration,
[2]
Lagrange equations
at a moment
computing
coordinate-independence of,
[2]
derivation of
as first-order system
for central potential (polar)
for central potential (rectangular)
for damped harmonic oscillator
for driven pendulum
for free rigid body
for gravitational potential
for harmonic oscillator,
[2]
for periodically driven pendulum
for spin-orbit coupling
from Newton's equations,
[2]
vs. Newton's equations
numerical integration of
off the beaten path
singularities in
traditional notation for,
[2]
uniqueness of solution
Lagrange-interpolation-function
Lagrange interpolation polynomial
Lagrange multiplier, see Lagrangian, augmented
Lagrange, Joseph Louis,
[2]
Lagrange-equations
Lagrangian
adding total time derivatives to
augmented, [2]
computing,
see also L-...
coordinate transformations of
cyclic in coordinate
energy and
for axisymmetric top
for central potential (polar),
[2]
for central potential (rectangular)
for central potential (spherical)
for constant acceleration
for damped harmonic oscillator
for driven pendulum,
[2]
for free particle
for free rigid body,
[2]
for gravitational potential
for harmonic oscillator
for spin-orbit coupling
for systems with rigid constraints
in generalized coordinates
generating functions and
Hamiltonian and,
[2]
kinetic energy as,
[2], [3]
kinetic minus potential energy as,
see also Hamilton's principle
non-uniqueness of
parameter names in
rotational and translational
symmetry of
Lagrangian action
Lagrangian formulation
Hamiltonian formulation and
Lagrangian reduction
Lagrangian state, see State tuple
Lagrangian state derivative
Lagrangian state path 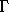 [q]
[q]
Lagrangian->energy
Lagrangian->Hamiltonian
Lagrangian->state-derivative
Lagrangian-action
lambda
Lambda calculus
Lambda expression
Lanczos, Cornelius
Least action, principle of, see Principle of stationary action
Legendre, Adrien Marie, see Legendre...
Legendre polynomials
Legendre-transform
Legendre transformation
active arguments in
passive arguments in
of quadratic functions
Leibniz, Gottfried
let
Libration of the Moon,
[2], [3]
Lie derivative
commutator for
Lie transform and
operator LH
Lie series
computing
for central field
for harmonic oscillator
in perturbation theory
Lie-transform
Lie transforms
advantage of
composition of
computing
exponential identities
for finding normal modes
Lie derivative and
in perturbation theory
Lie, Sophus, see Lie...
Lie-derivative,
[2]
Lindstedt, A.
Linear momentum
Linear separation of regular trajectories
Linear stability
equilibria and fixed points
nonlinear stability and
of equilibria
of fixed points
of inverted equilibrium of pendulum
Linear transformations as tuples
linear-interpolants
Liouville equation
Liouville's theorem
from canonical transformation
Liouville, Joseph, see Liouville...
Lipschitz condition (Rudolf Lipschitz)
Lisp
list
list-ref
Lists in Scheme
Literal symbol in Scheme
literal-function,
[2], [3],
[4]
Local names in Scheme
Local state tuple
Local tuple, [2]
 (chart) and
(chart) and
component names
functions of
in Scheme programs
transformation of (C)
Loops in Scheme
Lorentz, Hendrik Antoon, see Lorentz transformations
Lorentz transformations as point transformations
Lorenz, Edward
Lyapunov exponent
conserved quantities and
exponential divergence and
Hamiltonian constraints
linear stability and
Lyapunov, Alexey M., see Lyapunov exponent
M->omega-body
M-of-q->omega-of-t
MacCullagh's formula
make-path, [2]
Manifold
differentiable
stable and unstable
Map
area-preserving
Chirikov-Taylor
fixed points of,
see also Fixed points
Hénon's quadratic
Poincaré
representation in programs
standard
symplectic
twist
Mars, see Phobos
Mass point, see Point mass
Mathematical notation, see Notation
Mather, John N. (discoverer of sets named cantori by Ian Percival)
Matrix
inertia,
see also Inertia tensor
orthogonal
Pauli spin
symplectic, [2],
[3]
as tuple
Maupertuis, Pierre-Louis Moreau de,
[2]
Mean motion
Mechanics
Newtonian vs. variational formulation, [2]
Mercury, resonant rotation of,
[2]
Minimization
of action
in Scmutils, [2]
minimize
Moment(s) of inertia
about a line
about a pivot point
principal
of top
Momentum, see also Angular momentum
conjugate to coordinate, see Conjugate momentum
conservation of
generalized, see Generalized momentum
variation of
momentum
Momentum path
Momentum state function (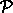 )
)
Moon
head-shaking
history of
libration of,
[2], [3]
rotation of,
[2], [3],
[4]
Moser, Jürgen, see Kolmogorov-Arnold-Moser theorem
Motion
atomic-scale
chaotic, see Chaotic motion
constrained,
see also Constraint(s)
dense, on torus
deterministic
epicyclic
ergodic
periodic, see Periodic motion
quasiperiodic, see Quasiperiodic motion
realizable vs. conceivable
regular vs. chaotic,
see also Regular motion
smoothness of
tumbling, see Chaotic motion, of Hyperion; Rotation(s), (in)stability of
multidimensional-minimize,
[2]
Multiplication of operators as composition
Multiplication of tuples
as composition
as contraction
Multiply-periodic functions, Poisson series for
Multipole expansion of potential energy
n-body problem
Nelder-Mead minimization method
Newton's equations
as Lagrange equations,
[2]
vs. Lagrange equations
Newton, Sir Isaac
Newtonian formulation of mechanics,
[2]
Noether, Emmy
Noether's theorem
angular momentum and
Non-associativity and associativity of tuple multiplication, [2]
Non-axisymmetric top
Non-commutativity, see also Commutativity
exponential(s) of noncommuting operators
of some partial derivatives,
[2]
of some tuple multiplication
Nonholonomic system
Nonsingular generalized coordinates
Nonsingular structure
Notation,
see also Subscripts; Superscripts; Tuples
{ }
( )
[ ], [2]
ambiguous
composition of functions
definite integral
derivative, partial:  ,
[2], [3]
,
[2], [3]
derivative: D,
[2]
derivative: 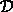
function of local tuple
functional, [2]
functional arguments
selector function: Ii, Iz,
[2]
total time derivative: Dt
traditional, [2],
[3], [4],
[5], [6]
Numbers in Scheme
Numerical integration
of Hamilton's equations
of Lagrange equations
in Scmutils, [2],
[3]
symplectic
Numerical minimization in Scmutils,
[2]
Nutation of top, [2]
Oblateness
*ode-integration-method*
omega (symplectic 2-form)
omega-cross
Operator
arithmetic operations on,
[2]
exponential identities
function vs.,
[2]
generic
Operators
derivative (D), see Derivative
Euler-Lagrange ( E )
Lie derivative (LH)
Lie transform (E' , W)
, W)
partial derivative ( ), see Partial derivative
), see Partial derivative
variation (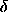
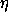 )
)
Optical libration of the Moon
Optics
Fermat
Snell's law
Orbit, see Phase-space trajectory
Orbital elements
Orbital motion, see also Epicyclic motion; Kepler problem
Lagrange equations for
retrodiction of
Orientation, see also Rotation(s)
Euler's equations and
nonsingular coordinates for
specified by Euler angles
specified by rotations
Orientation vector
Orthogonal matrix
Orthogonal transformation, see Orthogonal matrix
Orthogonal tuple-valued functions
Oscillator, see Harmonic oscillator
osculating-path
Osculation of paths
Ostrogradsky, M. V.
Out-of-roundness parameter
P (momentum selector),
[2]
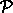 (momentum state function)
(momentum state function)
p->r (polar-to-rectangular)
pair?
Pairs in Scheme
Parallel tuple-valued functions
Parametric path
parametric-path-action
with graph
Parentheses
in Scheme, [2]
for up tuples
partial
Partial derivative,
[2], [3]
chain rule, [2]
notation:  ,
[2], [3]
,
[2], [3]
Particle, free, see Free particle
Path
coordinate path (q),
see also Local tuple
finding
momentum path
osculation of
parametric
realizable, see Realizable path
variation of, [2],
[3]
Path functions, abstraction of
Path-distinguishing function,
[2], see also Action
Pauli spin matrices (Wolfgang Pauli)
Peak
Pendulum, see also Pendulum (driven); Periodically driven pendulum
behavior of,
[2]
constraints and
degrees of freedom of
double (planar),
[2]
double (spherical)
equilibria, stable and unstable
Hamiltonian for
Lagrangian for
periodically driven pendulum vs.
as perturbed rotor
phase plane of,
[2]
phase-volume conservation for
spherical, [2]
width of oscillation region
Pendulum (driven),
see also Pendulum; Periodically driven pendulum
canonical gauge transformation and
drive as modification of gravity
Hamiltonian for,
[2]
Lagrange equations for
Lagrangian for,
[2]
Pericenter
Period doubling
Periodic motion
fixed points and
integrable systems and,
[2]
Periodic points
Poincaré-Birkhoff theorem
rational rotation number and
resonance islands and
Periodically driven pendulum, see also Pendulum (driven); Pendulum
behavior of,
[2]
chaotic behavior of
emergence of divided phase space
Hamiltonian for,
[2]
inverted equilibrium,
[2], [3],
[4]
islands in sections for,
[2], [3]
Lagrange equations for
linear stability analysis
as perturbed rotor
phase space evolution of
phase-space descriptions for
resonances for
spin-orbit coupling and
surface of section for,
[2], [3],
[4]
undriven pendulum vs.
with zero-amplitude drive
Periodically driven systems, surfaces of section
Perturbation of action-angle Hamiltonian, [2]
Perturbation theory
for many degrees of freedom
for pendulum
for periodically driven pendulum
for spin-orbit coupling
higher-order,
[2]
Lie series in
nonlinear resonance
secular terms in
secular-term elimination
small denominators in
Phase portrait, [2]
Phase space,
see also Surface of section
chaotic regions
divided, [2],
[3]
evolution in,
see also Time evolution of state
extended
non-uniqueness
of pendulum,
[2]
qualitative features,
[2], [3]
reduced
regular regions
two-dimensional
volume, see Phase-volume conservation
phase-space-derivative
Phase space reduction
conserved quantities and
Lagrangian
Phase-space state function
in Scheme
Phase-space trajectory (orbit)
asymptotic, [2],
[3]
chaotic, [2]
periodic, [2],
[3]
quasiperiodic,
[2]
regular, [2]
regular vs. chaotic
Phase-volume conservation,
[2]
for damped harmonic oscillator
for pendulum
under canonical transformations
Phobos, rotation of
Pit
Planets, see also Earth; Jupiter; Mercury
moment of inertia of
rotation of
rotational alignment of
plot-parametric-fill
plot-point
Plotting, [2],
[3]
Poe, Edgar Allan, see Pit; Pendulum
Poincaré, Henri,
[2], [3],
[4], [5]
Poincaré integral invariants
generating functions and
Poincaré map
Poincaré recurrence
Poincaré section, see Surface of section
Poincaré-Birkhoff theorem
computing fixed points
recursive nature of
Poincaré-Cartan integral invariant
time evolution and
Point mass,
see also Golf ball, tiny
Point transformations,
see also Canonical transformations
computing
general canonical transformations vs.
generating functions for
polar-rectangular conversion,
[2]
to rotating coordinates,
[2]
time-independent
Poisson brackets
commutator and
of conserved quantities
as derivations
fundamental
Hamilton's equations in terms of
in terms of 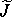
in terms of symplectic 2-form, 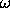
invariance under canonical transformations
Jacobi identity for
Lie derivative and
symplectic transformations and
Poisson series
for multiply periodic function
resonance islands and
Poisson, Siméon Denis
Polar coordinates
Lagrangian in
point transformation to rectangular, [2]
transformation to rectangular
polar-canonical
Polar-canonical transformation
generating function for
harmonic oscillator and
Potential, see Central force; Gravitational potential
Potential energy
for axisymmetric top
Hénon-Heiles
in Lagrangian
multipole expansion of
Precession
of equinox
of top, [2],
[3]
Predicate in conditional
Predicting the past
Principal axes
of this dense book
Principal moments of inertia
kinetic energy in terms of,
[2], [3]
principal-value
Principle of d'Alembert-Lagrange
Principle of least action, see Principle of stationary action
Principle of stationary action (action principle)
Hamilton's equations and
principle of least action,
[2]
statement of
used to find paths
print-expression,
[2]
Probability density in phase space
Procedure calls
Procedures
arithmetic operations on
generic
Products of inertia
Q (coordinate selector)
q (coordinate path)
qcrk4 (quality-controlled Runge-Kutta)
Quadratic functions, Legendre transformation of
Quadrature, [2],
see also Integrable systems
integrable systems and
reduction to
Quartet
Quasiperiodic motion,
[2]
Quaternions
Hamilton's discovery of
Quotation in Scheme
Radial momentum
Reaction force, see Constraint force
Realizable path
conserved quantities and
as solution of Hamilton's equations
as solution of Lagrange equations
stationary action and
uniqueness
Recurrence theorem of Poincaré
Recursive procedures
Reduced mass
Reduced phase space
Reduction
Lagrangian
of phase space, see Phase space reduction
to quadrature
ref, [2]
Regular motion, [2],
[3]
linear separation of trajectories
Renormalization
Resonance, see also Commensurability
center
islands, see Islands in surfaces of section
nonlinear
of Mercury's rotation,
[2]
overlap criterion,
[2]
for periodically driven pendulum
width, [2]
Rigid body
forced,
see also Spin-orbit coupling; Top
free, see Rigid body (free)
kinetic energy
kinetic energy in terms of inertia tensor and angular velocity, [2]
kinetic energy in terms of principal moments and angular momentum
kinetic energy in terms of principal moments and angular velocity
kinetic energy in terms of principal moments and Euler angles
vector angular momentum
Rigid body (free)
angular momentum
angular momentum and kinetic energy
computing motion of
Euler's equations and
(in)stability
orientation
Rigid constraints
as coordinate transformations
Rotating coordinates
in extended phase space
generating function for
point transformation for,
[2]
Rotation number
golden
irrational, and invariant curves
rational, and commensurability
rational, and fixed and periodic points
Rotation(s), see also Orientation
active
composition of,
[2]
computing
group property of
(in)stability of
kinematics of
kinetic energy of, see Rigid body, kinetic energy...
Lie generator for
matrices for
of celestial objects,
[2], [3]
of Hyperion
of Mercury, [2]
of Moon, [2],
[3], [4]
of top, book, and Moon
orientation as
orientation vector and
passive
as tuples
Rotor
driven, [2]
pendulum as perturbation of
periodically driven pendulum as perturbation of
Routh, Edward John
Routhian
Routhian equations
Runge-Kutta integration method
qcrk4
S or S (action)
(action)
vs. 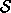
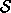 (action)
(action)
s->m (structure to matrix)
s->r (spherical-to-rectangular)
Saddle point
Salam, Abdus
Saturn, see Hyperion
Scheme, [2],
[3], see also Scmutils
for Gnu/Linux, where to get it
Schrödinger, Erwin,
[2]
Scmutils, [2],
see also Scheme
division by a structure
division of vector by matrix
generic arithmetic,
[2], [3]
minimization, [2]
numerical integration,
[2], [3]
operations on operators
simplification of expressions,
[2]
where to get it
Second law of thermodynamics
Section, surface of, see Surface of section
Secular terms in perturbation theory
elimination of
Selector function,
[2]
Selectors in Scheme
Semicolon in tuple,
[2]
Sensitivity to initial conditions,
[2], [3],
see also Chaotic motion
Separatrix, [2],
see also Asymptotic trajectories
chaos near, [2],
[3]
motion near
series
series:for-each
show-expression
Shuffle function 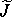
Simplification of expressions,
[2]
Singularities, [2],
[3]
nonsingular generalized coordinates
Sleeping top
Small denominators
for periodically driven pendulum
in perturbation theory,
[2]
resonance islands and,
[2]
Small divisors, see Small denominators
Snell's law
Solvable systems, see Integrable systems
Spherical coordinates
kinetic energy in
Lagrangian in
Spin matrices, Pauli
Spin-orbit coupling
chaotic motion,
[2]
Lagrange equations for
Lagrangian for
periodically driven pendulum and
perturbation theory for
surface of section for
Spivak, Michael, [2]
square
for tuples, [2]
Stability, see Equilibria; Instability; Linear stability
Stable manifold
computing
Standard map
standard-map
Stars, see Galaxy
State
evolution of, see Time evolution of state
Hamiltonian vs. Lagrangian
in terms of coordinates and momenta (Hamiltonian)
in terms of coordinates and velocities (Lagrangian)
State derivative
Hamiltonian
Hamiltonian vs. Lagrangian
Lagrangian
State path
Hamiltonian
Lagrangian
State tuple
state-advancer
Stationarity condition
Stationary action, see Principle of stationary action
Stationary point
Steiner's theorem
String theory, [2],
see also Quartet
Stroboscopic surface of section,
see also Surface of section
computing
Subscripts
down and
for down-tuple components
for momentum components,
[2]
for selectors
Summation convention
Superscripts
for coordinate components,
[2], [3]
for up-tuple components
for velocity components,
[2]
up and
Surface of section
in action-angle coordinates
area preservation of,
[2]
computing (Hénon-Heiles)
computing (stroboscopic)
fixed points, see Fixed points
for autonomous systems
for Hénon-Heiles problem
for integrable system
for non-axisymmetric top
for periodically driven pendulum,
[2], [3],
[4]
for spin-orbit coupling
invariant curves, see Invariant curves
islands, see Islands in surfaces of section
stroboscopic
Symbolic values
Symbols in Scheme
Symmetry
conserved quantities and,
[2]
continuous
of Lagrangian
of top
Symplectic bilinear form (2-form)
invariance under canonical transformations
Symplectic condition
Symplectic integration
Symplectic map
Symplectic matrix,
[2], [3]
Symplectic transformations,
see also Canonical transformations
antisymmetric bilinear form and
Poisson brackets and
Symplectic unit J, Jn,
[2]
symplectic-matrix?
symplectic-transform?
symplectic-unit
symplectic?
Syntactic sugar
System derivative, see State derivative
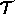 [
[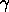 ]
]
T-rigid-body
Taylor, J. B.
Tensor arithmetic
notation and,
[2]
summation convention
tuple arithmetic vs.,
[2]
Theology and principle of least action
Thermodynamics, second law
Three-body problem, restricted
Tidal friction
time
Time evolution of state
action and, [2]
as canonical transformation
in phase space
Poincaré-Cartan integral invariant and
time-independent-canonical?
Time-dependent canonical transformations
Time-independence, see also Extended phase space
energy conservation and
Time-independent canonical transformations
Top
Axisymmetric, see Axisymmetric top
non-axisymmetric
Top banana, see Non-axisymmetric top
Torque
in Euler's equations
in spin-orbit coupling
Total time derivative
adding to Lagrangians
affecting conjugate momentum
commutativity of
computing
constraints and
identifying
notation: Dt
Trajectory, see Path; Phase-space trajectory
Transformation
canonical, see Canonical transformations
coordinate, see Coordinate transformations
Legendre, see Legendre transformation
Lie, see Lie transforms
orthogonal, see Orthogonal matrix
point, see Point transformations
symplectic, see Symplectic transformations
True anomaly
Tumbling, see Chaotic motion, of Hyperion; Rotation(s), (in)stability of
Tuples
arithmetic on,
[2]
commas and semicolons in
component selector: Ii, Iz,
[2]
composition and
contraction
of coordinates
down and up
of functions,
[2]
inner product
linear transformations as
local, see Local tuple
matrices as
multiplication of
rotations as
squaring, [2]
state tuple
up and down
Twist map
Two-body problem
Two-trajectory method
Undriven pendulum, see Pendulum
Uniform circle map
Uniqueness
of Lagrangian -- not!
of phase-space description -- not!
of realizable path
of solution to Lagrange equations
Unstable manifold
computing
up, [2]
Up tuples
Vakonomic mechanics
Variation
chain rule
of a function
of a path, [2],
[3]
of action
operator: 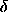
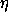
Variational equations
Variational formulation of mechanics,
[2]
Variational principle, see Principle of stationary action
Vector
body components of
in Scheme
square of
vector
Vector angular momentum,
see also Angular momentum
center-of-mass decomposition
in terms of angular velocity and inertia tensor
in terms of principal moments and angular velocity
in terms of principal moments and Euler angles
Vector space of tuples
Vector torque, see Torque
vector-ref
vector?
Velocity, see Angular velocity; Generalized velocity
velocity
Velocity dispersion in galaxy
Web site for this book
Whittaker transform (Sir Edmund Whittaker)
Zero-amplitude drive for pendulum
Zero-based indexing,
[2], [3],
[4], [5]
 (``chart'' function)
(``chart'' function)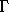 [q]
[q]
 L[q] (Hamiltonian state path)
L[q] (Hamiltonian state path) (coordinate function)
(coordinate function)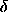 function
function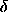
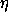 (variation operator)
(variation operator)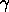 (configuration-path function)
(configuration-path function)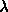 -calculus
-calculus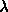 -expression
-expression -notation
-notation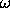 matrix
matrix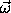 (angular velocity)
(angular velocity)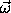 (t) × operator
(t) × operator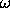 (symplectic 2-form)
(symplectic 2-form)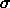 (phase-space path)
(phase-space path) vs. D
vs. D , see Partial derivative
, see Partial derivative
 (energy state function)
(energy state function) (shuffle function)
(shuffle function) (Lagrangian)
(Lagrangian)
 (Lagrangian)
(Lagrangian)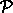 (momentum state function)
(momentum state function) (action)
(action)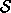
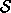 (action)
(action)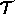 [
[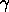 ]
] )
)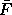
 (chart) and
(chart) and , W)
, W)