Exercise 1.38. A numerical investigation
Consider a pendulum: a mass m supported on a massless rod of length l
in a uniform gravitational field. A Lagrangian for the pendulum
is

For the pendulum, the period of the motion depends on the amplitude. We wish to find trajectories of the pendulum with a given frequency. Three methods of doing this present themselves: (1) solution by the principle of least action, (2) numerical integration of Lagrange's equation, and (3) analytic solution (which requires some exposure to elliptic functions). We will carry out all three and compare the solution trajectories.
Consider the parameters m = 1 kg, l = 1 m,
g = 9.8 m s-2. The frequency of small-amplitude oscillations is
 0 = (g/l)1/2. Let's find the nontrivial solution that has the
frequency
0 = (g/l)1/2. Let's find the nontrivial solution that has the
frequency  1 = (4/5)
1 = (4/5)  0.
0.
a. The angle is periodic in time, so a Fourier series representation is appropriate. We can choose the origin of time so that a zero crossing of the angle is at time zero. Since the potential is even in the angle, the angle is an odd function of time. Thus we need only a sine series. Since the angle returns to zero after one-half period, the angle is an odd function of time about the midpoint. Thus only odd terms of the series are present:

The amplitude of the trajectory is A =  max = sumn=1infty ( - 1)n+1 An.
max = sumn=1infty ( - 1)n+1 An.
Find approximations to the first few coefficients An by minimizing the action. You will have to write a program similar to the find-path procedure in section 1.4. Watch out: there is more than one trajectory that minimizes the action.
b. Write a program to numerically integrate Lagrange's equations for
the trajectories of the pendulum. The trouble with using numerical
integration to solve this problem is that we do not know how the
frequency of the motion depends on the initial conditions. So we have
to guess, and then gradually improve our guess. Define a function
 (
( ) that numerically computes the frequency of the
motion as a function of the initial angular velocity (with
) that numerically computes the frequency of the
motion as a function of the initial angular velocity (with  =
0). Find the trajectory by solving
=
0). Find the trajectory by solving  (
( ) =
) =  for the initial angular velocity of the desired trajectory. Methods
of solving this equation include successive bisection, minimizing the
squared residual, etc. -- choose one.
for the initial angular velocity of the desired trajectory. Methods
of solving this equation include successive bisection, minimizing the
squared residual, etc. -- choose one.
c. Now let's formulate the analytic solution for the frequency as a function of amplitude. The period of the motion is simply

Using the energy, solve for  in terms of the amplitude
A and
in terms of the amplitude
A and  to write the required integral explicitly. This
integral can be written in terms of elliptic functions, but in a sense
this does not solve the problem -- we still have to compute the
elliptic functions. Let's avoid this excursion into elliptic
functions and just do the integral numerically using the procedure
definite-integral. We still have the problem that we can
specify the amplitude A and get the frequency; to solve our
problem we need to solve the inverse problem, but that can be done as
in part b.
to write the required integral explicitly. This
integral can be written in terms of elliptic functions, but in a sense
this does not solve the problem -- we still have to compute the
elliptic functions. Let's avoid this excursion into elliptic
functions and just do the integral numerically using the procedure
definite-integral. We still have the problem that we can
specify the amplitude A and get the frequency; to solve our
problem we need to solve the inverse problem, but that can be done as
in part b.
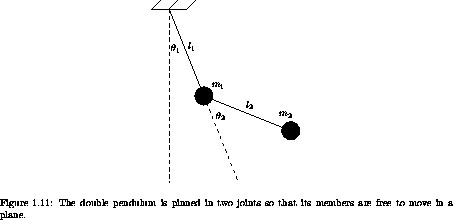
Exercise 1.39. Double pendulum behavior
Consider the ideal double
pendulum shown in figure 1.11.
a. Formulate a Lagrangian to describe the dynamics.
Derive the equations of motion in terms of the given angles
 1 and
1 and  2. Put the equations into a form appropriate
for numerical integration. Assume the following system parameters:
2. Put the equations into a form appropriate
for numerical integration. Assume the following system parameters:
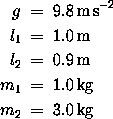
b. Prepare graphs showing the behavior of each angle as a function of time when the system is started with the following initial conditions:
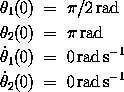
Make the graphs extend to 50 seconds. Save the state points at .125-second intervals in a list.
c. Make a graph of the behavior of the energy of your system as a function of time. The energy should be conserved. How good is the conservation you obtained?
d. Repeat the experiment of part b with the m2 bob 10-10 m higher than before. Form the list of squared differences of the distances between the m2 bobs in the two experiments, and plot the log of that against time. What do you see?
e. Repeat the previous comparison, but this time with the initial conditions:

What do you see here?