
In this section we demonstrate that time evolution generates a canonical transformation: if we consider all possible initial states of a Hamiltonian system and follow all the trajectories for the same time interval, then the map from the initial state to the final state of each trajectory is a canonical transformation.
We use time evolution to generate a transformation

that is obtained in the following way. Let 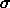 (t) = (t,
(t) = (t,  (t),
(t),
 (t)) be a solution of Hamilton's equations. The transformation
(t)) be a solution of Hamilton's equations. The transformation

 satisfies
satisfies


Notice that 
 changes the time component. This is the
first transformation of this kind that we have considered.24
changes the time component. This is the
first transformation of this kind that we have considered.24
Given a state (t', q', p'), we find the phase-space path 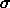 emanating from this state as an initial condition, satisfying
emanating from this state as an initial condition, satisfying

The value (t, q, p) of 
 (t', q', p') is then
(t' +
(t', q', p') is then
(t' +  ,
,  (t' +
(t' +  ),
),  (t' +
(t' +  )).
)).
Time evolution is canonical if the transformation 
 is symplectic and if the Hamiltonian transforms in an appropriate
manner. The transformation
is symplectic and if the Hamiltonian transforms in an appropriate
manner. The transformation 
 is symplectic if the
bilinear antisymmetric form
is symplectic if the
bilinear antisymmetric form  is invariant (see
equation 5.73) for a general pair of
linearized state variations with zero time component.
is invariant (see
equation 5.73) for a general pair of
linearized state variations with zero time component.
Let  ' be an increment with zero time component of the state
(t', q', p'). The linearized increment in the value of
' be an increment with zero time component of the state
(t', q', p'). The linearized increment in the value of 
 (t', q', p') is
(t', q', p') is  = D
= D
 (t', q', p')
(t', q', p')
 '. The image of the increment is obtained by multiplying the
increment by the derivative of the transformation. On the other hand,
the transformation is obtained by time evolution, so the image of the
increment can also be found by the time evolution of the linearized
variational system.
Let
'. The image of the increment is obtained by multiplying the
increment by the derivative of the transformation. On the other hand,
the transformation is obtained by time evolution, so the image of the
increment can also be found by the time evolution of the linearized
variational system.
Let

be variations of the state path 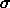 (t) = (t,
(t) = (t,  (t),
(t),  (t));
then
(t));
then


This must be true for arbitrary  , so it is satisfied if the following quantity is constant:
, so it is satisfied if the following quantity is constant:


With Hamilton's equations, the variations satisfy

Substituting these into DA and collecting terms, we find25

We conclude that time evolution generates a phase-space transformation with symplectic derivative.
To make a canonical transformation we must specify how the Hamiltonian transforms. The same Hamiltonian describes the evolution of a state and a time-advanced state because the latter is just another state. Thus the transformed Hamiltonian is the same as the original Hamiltonian.
We deduced that volumes in phase space are preserved by time evolution by showing that the divergence of the phase flow is zero, using the equations of motion (see section 3.8). We can also show that volumes in phase space are preserved by the evolution using the fact that time evolution is a canonical transformation.
We have shown that phase-space volume is preserved for symplectic transformations. Now we have shown that the transformation generated by time evolution is a symplectic transformation. Therefore, the transformation generated by time evolution preserves phase-space volume. This is an alternate proof of Liouville's theorem.
There is another canonical transformation that can be constructed from
time evolution. We define the transformation  '
' such
that
such
that

where S (a, b, c) = (a +
(a, b, c) = (a +  , b, c) shifts the time
of a phase-space state.26
More explicitly, given a state (t, q', p'), we evolve the state
that is obtained by subtracting
, b, c) shifts the time
of a phase-space state.26
More explicitly, given a state (t, q', p'), we evolve the state
that is obtained by subtracting  from t; that is, we take the state
(t -
from t; that is, we take the state
(t -  , q', p') as an initial state for evolution by Hamilton's
equations. The state path
, q', p') as an initial state for evolution by Hamilton's
equations. The state path 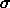 satisfies
satisfies

The output of the transformation is the state


The arguments of  '
' are not a consistent phase-space
state; the time argument must be decremented by
are not a consistent phase-space
state; the time argument must be decremented by  to obtain a
consistent state. The transformation is completed by evolution of
this consistent state.
to obtain a
consistent state. The transformation is completed by evolution of
this consistent state.
Why is this a good idea? Our usual canonical transformations do not change the time component. This modified time-evolution transformation is thus of the form discussed previously. The resulting time-evolution transformation is canonical and in the usual form:

This transformation can also be extended to
be a canonical transformation,
with an appropriate adjustment of the Hamiltonian. The Hamiltonian
H' that gives the correct Hamilton's equations at the
transformed phase-space point is the original Hamiltonian composed
with a function that decrements the independent variable by
that gives the correct Hamilton's equations at the
transformed phase-space point is the original Hamiltonian composed
with a function that decrements the independent variable by  :
:


Notice that if H is time independent then H' = H.
= H.
Assume we have a procedure C such that ((C delta-t) state)
implements a time-evolution transformation 
 of the state state
with time interval delta-t;
then the procedure Cp such that ((Cp delta-t) state) implements
of the state state
with time interval delta-t;
then the procedure Cp such that ((Cp delta-t) state) implements
 '
' of the same state and time interval can be derived from the procedure C by using the procedure
of the same state and time interval can be derived from the procedure C by using the procedure
(define ((C->Cp C) delta-t)
(compose (C delta-t) (shift-t (- delta-t))))
where shift-t implements S :
:
(define ((shift-t delta-t) state)
(up
(+ (time state) delta-t)
(coordinate state)
(momentum state)))
To complete the canonical transformation we have a procedure that transforms the Hamiltonian:
(define ((H->Hp delta-t) H)
(compose H (shift-t (- delta-t))))
So both  and
and  ' can be used to make canonical
transformations by specifying how the old and new Hamiltonians are
related. For
' can be used to make canonical
transformations by specifying how the old and new Hamiltonians are
related. For 
 the Hamiltonian is unchanged. For
the Hamiltonian is unchanged. For
 '
' the Hamiltonian is time shifted.
the Hamiltonian is time shifted.
Exercise 5.21. Verification
The condition (5.19) that Hamilton's
equations are preserved for 
 is
is

and the condition that Hamilton's
equations are preserved for  '
' is
is

Verify that these conditions are satisfied.
Exercise 5.22. Driven harmonic oscillator
We can use the simple driven harmonic oscillator to illustrate that
time evolution yields a symplectic transformation that can be
extended to be canonical in two ways. We use the driven harmonic
oscillator because its solution can be compactly expressed in explicit
form.
Suppose that we have a harmonic oscillator with natural frequency
 0 driven by a periodic sinusoidal drive of frequency
0 driven by a periodic sinusoidal drive of frequency  and amplitude
and amplitude  . The Hamiltonian we will consider is
. The Hamiltonian we will consider is

The general solution for a given initial state (t0, q0, p0)
evolved for a time  is
is

where  ' =
' =  /(
/( 02 -
02 -  2).
2).
a. Fill in the details of the procedure
(define (((C alpha omega omega0) delta-t) state)
... )
that implements the time-evolution transformation of the driven harmonic oscillator.
b. In terms of C, the general solution emanating from a given state is
(define (((solution alpha omega omega0) state0) t)
(((C alpha omega omega0) (- t (time state0))) state0))
Check that the implementation of C is correct by using it to construct the solution and verifying that the solution satisfies Hamilton's equations. Further check the solution by comparing to numerical integration.
c. We know that for any phase-space state function F the rate of change
of that function along a solution path 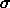 is
is

Show, by writing a short program to test it, that this is true of the function implemented by (C delta) for the driven oscillator. Why is this interesting?
d. Verify that both C and Cp are symplectic using symplectic?.
e. Use the procedure canonical? to verify that both C and Cp are canonical with the appropriate transformed Hamiltonian.
We can also show that time evolution generates canonical transformations using the Poincaré-Cartan integral invariant.
Consider a two-dimensional region of phase-space coordinates, R', at
some particular time t' (see figure 5.8). Let R be the
image of this region at time t under time evolution for a time
interval of  . The time evolution is governed by a Hamiltonian
H. Let sumi Ai be the sum of the oriented areas of the
projections of R onto the fundamental canonical planes.27
Similarly, let sumi A'i be the sum of oriented projected areas for
R'. We will show that sumi Ai = sumi A'i, and thus the
Poincaré integral invariant is preserved by time evolution. By
showing that the Poincaré integral invariant is preserved, we will
have shown that the qp part of the transformation generated by time
evolution is symplectic. From this we can construct canonical
transformations from time evolution as before.
. The time evolution is governed by a Hamiltonian
H. Let sumi Ai be the sum of the oriented areas of the
projections of R onto the fundamental canonical planes.27
Similarly, let sumi A'i be the sum of oriented projected areas for
R'. We will show that sumi Ai = sumi A'i, and thus the
Poincaré integral invariant is preserved by time evolution. By
showing that the Poincaré integral invariant is preserved, we will
have shown that the qp part of the transformation generated by time
evolution is symplectic. From this we can construct canonical
transformations from time evolution as before.
In the extended phase space we see that the evolution sweeps out a cylindrical volume with endcaps R' and R, each at a fixed time. Let R'' be the two-dimensional region swept out by the trajectories that map the boundary of region R' to the boundary of region R. The regions R, R', and R'' together form the boundary of a volume of phase-state space.
The Poincaré-Cartan integral invariant on the whole boundary is zero.28 Thus

where the n index indicates the t, pt canonical plane. The second term is negative, because in the extended phase space we take the area to be positive if the normal to the surface is outward pointing.

We will show that the Poincaré-Cartan integral invariant for a region of phase space that is generated by time evolution is zero:

This will allow us to conclude

The areas of the projection of R and R' on the t, pt plane are zero because R and R' are at constant times, so for these regions the Poincaré-Cartan integral invariant is the same as the Poincaré integral invariant. Thus

We are left with showing that the Poincaré-Cartan integral invariant
for the region R'' is zero. This will be zero if the contribution
from any small piece of R'' is zero. We will show this by showing
that the  form (see equation 5.71) on a small
parallelogram in this region
is zero. Let (0; q, t; p, pt) be a vertex of this parallelogram. The
parallelogram is specified by two edges
form (see equation 5.71) on a small
parallelogram in this region
is zero. Let (0; q, t; p, pt) be a vertex of this parallelogram. The
parallelogram is specified by two edges  1 and
1 and  2
emanating from this vertex with components (0;
2
emanating from this vertex with components (0;  q,
q,  t;
t;
 p,
p,  pt). For edge
pt). For edge  1 of the parallelogram, we take
a constant-time phase-space increment with length
1 of the parallelogram, we take
a constant-time phase-space increment with length  q and
q and
 p in the q and p directions. The first-order change in
the Hamiltonian that corresponds to these changes is
p in the q and p directions. The first-order change in
the Hamiltonian that corresponds to these changes is

for constant time  t = 0. The increment
t = 0. The increment  pt is the
negative of
pt is the
negative of  H. So the extended phase-space increment is
H. So the extended phase-space increment is

The edge  2 is obtained by time evolution of the vertex for a
time interval
2 is obtained by time evolution of the vertex for a
time interval  t. Using Hamilton's equations, we obtain
t. Using Hamilton's equations, we obtain

The  form applied to these incremental states that form the
edges of this parallelogram gives the area of the parallelogram:
form applied to these incremental states that form the
edges of this parallelogram gives the area of the parallelogram:

So we may conclude that the integral of this expression over the entire surface of the tube of trajectories is also zero. Thus the Poincaré-Cartan integral invariant is zero for any region that is generated by time evolution.
Having proven that the trajectory tube provides no contribution, we have shown that the Poincaré integral invariant of the two endcaps is the same. This proves that time evolution generates a symplectic qp transformation.
We can use the Poincaré-Cartan invariant to prove that for autonomous two-degree-of-freedom systems surfaces of section (constructed appropriately) preserve area.
To show this we consider a surface of section for one coordinate (say q2) equal to zero. We construct the section by accumulating the (q1, p1) pairs. We assume that all initial conditions have the same energy. We compute the sum of the areas of canonical projections in the extended phase space again. Because all initial conditions have the same q2 = 0 there is no area on the q2, p2 plane, and because all the trajectories have the same value of the Hamiltonian the area of the projection on the t, pt plane is also zero. So the sum of areas of the projections is just the area of the region on the surface of section. Now let each point on the surface of section evolve to the next section crossing. For each point on the section this may take a different amount of time. Compute the sum of the areas again for the mapped region. Again, all points of the mapped region have the same q2 so the area on the q2, p2 plane is zero, and they continue to have the same energy so the area on the t, pt plane is zero. So the area of the mapped region is again just the area on the surface of section, the q1, p1 plane. Time evolution preserves the sum of areas, so the area on the surface of section is the same as the mapped area.
So surfaces of section preserve area provided that the section points are entirely on a canonical plane. For example, to make the Hénon-Heiles surfaces of section (see section 3.6.3) we plotted py versus y when x = 0 with px > 0. So for all section points the x coordinate has the fixed value 0, the trajectories all have the same energy, and the points accumulated are entirely in the y, py canonical plane. So the Hénon-Heiles surfaces of section preserve area.
We can show that time evolution generates a symplectic transformation directly from the action principle.
Recall that the Lagrangian action S is

We computed the variation of the action in deriving the Lagrange equations. The variation is (see equation 1.33)

rewritten in terms of the Euler-Lagrange operator E. In the
derivation of the Lagrange equations we considered only variations
that preserved the endpoints of the path being tested. However,
equation (5.347) is true of arbitrary variations.
Here we consider variations that are not zero at the endpoints
around a realizable path q (one for which
E [ L ] o 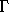 [q] = 0 ). For these variations
the variation of the action is just the integrated term:
[q] = 0 ). For these variations
the variation of the action is just the integrated term:

Recall that p and 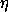 are structures, and the product implies a
sum of products of components.
are structures, and the product implies a
sum of products of components.
Consider a continuous family of realizable paths; the path for parameter s is
 (s) and the coordinates of this path at time t are
(s) and the coordinates of this path at time t are
 (s)(t).
We define
(s)(t).
We define  (s) = D
(s) = D (s); the variation of the path
along the family is the
derivative of the parametric path with respect to the parameter.
Let
(s); the variation of the path
along the family is the
derivative of the parametric path with respect to the parameter.
Let

be the value of the action from t1 to t2 for path  (s).
The derivative of the action along this parametric family of paths is29
(s).
The derivative of the action along this parametric family of paths is29

Because  (s) is
a realizable path, E[L] o
(s) is
a realizable path, E[L] o 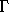 [
[ (s)] = 0. So
(s)] = 0. So

where  (s) is the conjugate momentum to
(s) is the conjugate momentum to  (s).
The integral of D
(s).
The integral of D is
is


In conventional notation the latter line integral is written

where  1(s) =
1(s) =  (s)(t1) and
(s)(t1) and  2(s) =
2(s) =  (s)(t2).
(s)(t2).
For a loop family of paths (such that  (s2) =
(s2) =  (s1)), the
difference of actions at the endpoints vanishes, so we deduce
(s1)), the
difference of actions at the endpoints vanishes, so we deduce

which is the line-integral version of the integral invariants.
In terms of area integrals, using Stokes's theorem, this is

where Rij are the regions in the ith canonical plane. We have found that the time evolution preserves the integral invariants, and thus time evolution generates a symplectic transformation.
24 Our theorems about which transformations are canonical are still valid, because they required only that the derivative of the independent variable be 1.
25 Partial derivatives of structured arguments do not generally commute, so this deduction is not as simple as it may appear. It is helpful to introduce component indices and consider the equation componentwise.
26 The transformation S is an identity on the qp
components, so it is symplectic. Although it adjusts the time, it
is not a time-dependent transformation in that the qp components
do not depend upon the time. Thus, if we adjust the Hamiltonian by
composition with S
is an identity on the qp
components, so it is symplectic. Although it adjusts the time, it
is not a time-dependent transformation in that the qp components
do not depend upon the time. Thus, if we adjust the Hamiltonian by
composition with S we have a canonical transformation.
we have a canonical transformation.
27 By Stokes's theorem we may compute the area of a region by a line integral around the boundary of the region. We define the positive sense of the area to be the area enclosed by a curve that is traversed in a counterclockwise direction, when drawn on a plane with the coordinate on the abscissa and the momentum on the ordinate.
28 We can see this as follows.
Let  be any closed curve in the boundary. This curve divides
the boundary into two regions. By Stokes's theorem the integral
invariant over both of these pieces can be written as a line integral
along this boundary, but they have opposite signs, because
be any closed curve in the boundary. This curve divides
the boundary into two regions. By Stokes's theorem the integral
invariant over both of these pieces can be written as a line integral
along this boundary, but they have opposite signs, because  is
traversed in opposite directions to keep the surface on the left. So
we conclude that the integral invariant over the entire surface is zero.
is
traversed in opposite directions to keep the surface on the left. So
we conclude that the integral invariant over the entire surface is zero.
29 Let f be a path-dependent function,
 (s) = D
(s) = D (s), and g(s) =
f[
(s), and g(s) =
f[ (s)]. The variation of f at
(s)]. The variation of f at  (s)
in the direction
(s)
in the direction  (s) is
(s) is
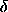
 (s) f[
(s) f[ (s)] = D g(s).
(s)] = D g(s).