Exercise 2.20. Free rigid body
Write and demonstrate a program that reproduces diagrams like
figure 2.3 (section 2.9.2). Can you find trajectories that are
asymptotic to the unstable relative equilibrium on the intermediate
principal axis?
Exercise 2.21. Rotation of Mercury
In the '60s it was discovered that Mercury has a rotation period that
is precisely 2/3 times its orbital period. We can see this resonant
behavior in the spin-orbit model problem, and we can also play with nudging
Mercury a bit to see how far off the rotation rate can be and still be
trapped in this spin-orbit resonance. If the mismatch in angular
velocity is too great, Mercury's rotation is no longer resonantly
locked to its orbit. Set  = 0.026 and e = 0.2.
= 0.026 and e = 0.2.
a. Write a program for the spin-orbit problem so this resonance
dynamics can be investigated numerically. You will need to know (or,
better, show!) that f satisfies the equation
with
Notice that n disappears from the equations if they are written in terms
of a new independent variable  = n t. Also notice that
a and R(t) appear only in the combination a/R(t).
= n t. Also notice that
a and R(t) appear only in the combination a/R(t).
b. Show that the 3:2 resonance is stable by numerically
integrating the system when the rotation is not exactly in resonance
and observing that the angle  - (3/2) nt
oscillates.
- (3/2) nt
oscillates.
c. Find the range of initial  for which this
resonance angle oscillates.
for which this
resonance angle oscillates.
 = 0.026 and e = 0.2.
= 0.026 and e = 0.2. 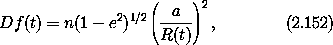
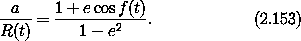
 = n t. Also notice that
a and R(t) appear only in the combination a/R(t).
= n t. Also notice that
a and R(t) appear only in the combination a/R(t). - (3/2) nt
oscillates.
- (3/2) nt
oscillates.  for which this
resonance angle oscillates.
for which this
resonance angle oscillates.