
For a free rigid body we have seen that the components of the angular momentum on the principal axes comprise a self-contained dynamical system: the variation of the principal axis components depends only on the principal axis components. Here we derive equations that govern the evolution of these components.
The starting point for the derivation is the conservation of the vector angular momentum. The components of the angular momentum on the principal axes are

where  ' is composed of the components of the angular velocity
vector on the principal axes and I' is the matrix
representation of the inertia tensor with respect to the principal
axis basis:
' is composed of the components of the angular velocity
vector on the principal axes and I' is the matrix
representation of the inertia tensor with respect to the principal
axis basis:

The body components of the angular momentum L' are related to the
components L on the fixed rectangular basis  i by
i by

where M is the matrix representation of the rotation that carries the body and all vectors attached to the body from the reference orientation of the body to the actual orientation.
The vector angular momentum is conserved for free rigid-body motion, and so are its components on a fixed rectangular basis. So, along solution paths,
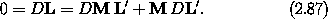
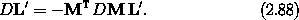
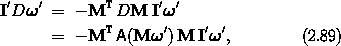
where we have used equation (2.38) to write DM in terms of A. The function A has the property20
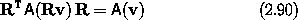
for any vector with components v and any rotation with matrix representation R. Using this property of A, we find Euler's equations:
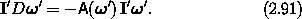
Euler's equations give
the time derivative of the body components of
the angular velocity vector entirely in terms of the angular velocity
components and the principal moments of inertia.
Let  a,
a,
 b, and
b, and  c denote the components of the angular
velocity vector on the principal axes. Then Euler's equations can be written
as the component equations
c denote the components of the angular
velocity vector on the principal axes. Then Euler's equations can be written
as the component equations
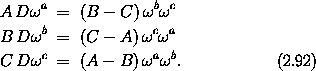
Alternately, we can rewrite Euler's equations in terms of the components of the angular momentum on the principal axes

These equations confirm that the time derivatives of the components of the angular momentum on the principal axes depend only on the components of the angular momentum on the principal axes.
Euler's equations are very simple, but they do not completely determine the evolution of a rigid body -- they do not give the spatial orientation of the body. However, equation (2.38) and property (2.90) can be used to relate the derivative of the orientation matrix to the body components of the angular velocity vector:

A straightforward method of using these equations is to integrate them
componentwise as a set of nine first-order ordinary differential
equations, with initial conditions determining the initial
configuration matrix. Together with Euler's equations, which describe
how the body components of the angular velocity vector change with
time, this system of equations governing the motion of a rigid body is
complete. However, the reader will no doubt have noticed that this
approach is rather wasteful. The fact that the orientation matrix can
be specified with only three parameters has not been taken into
account. We should be integrating three equations for the
orientation, given  ', not nine. To accomplish this we once
again need to parameterize the configuration
matrix.
', not nine. To accomplish this we once
again need to parameterize the configuration
matrix.
For example, we can use Euler angles to parameterize the orientation:
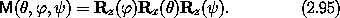
We form M by composing M with an Euler coordinate path.
Equation (2.94) can then be used to solve for
D , D
, D , and D
, and D . We find
. We find
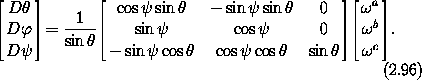
This gives us the desired equation for the orientation. Note that it
is singular for  = 0, as are Lagrange's equations. So Euler's
equations using Euler angles for the configuration have the same
problem as did the Lagrange equations using Euler angles. Again, this
is a manifestation of the fact that for
= 0, as are Lagrange's equations. So Euler's
equations using Euler angles for the configuration have the same
problem as did the Lagrange equations using Euler angles. Again, this
is a manifestation of the fact that for  = 0 the orientation depends
only on
= 0 the orientation depends
only on  +
+  . The singularity in the equations of motion for
. The singularity in the equations of motion for
 = 0 does not correspond to anything funny in the motion of the
rigid body. A practical solution to the singularity problem is to
choose another set of Euler-like angles that have a singularity in a
different place, and switch from one to the other when the going gets
tough.
= 0 does not correspond to anything funny in the motion of the
rigid body. A practical solution to the singularity problem is to
choose another set of Euler-like angles that have a singularity in a
different place, and switch from one to the other when the going gets
tough.
Exercise 2.15.
Fill in the details of the derivation of
equation (2.96). You may want to use the
computer to help with the algebra.
Euler's equations were derived for a free rigid body. In general, we must be able to deal with external forcing. How do we do this? First, we derive expressions for the vector torque. Then we include the vector torque in the Euler equations.
We derive the vector torque in a manner analogous to the derivation of the vector angular momentum. That is, we derive one component and then argue that since the coordinate system is arbitrary, all components have the same form.
Suppose we have a rigid body subject to some potential energy that depends
only on time and the configuration. A Lagrangian
is L = T - V.
If we use the Euler angles as generalized coordinates, the last of the
three active Euler rotations that define the
orientation is a rotation about the 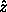 axis. The magnitude of
this rotation is given by the angle
axis. The magnitude of
this rotation is given by the angle  . The
Lagrange equation for
. The
Lagrange equation for  gives21
gives21

If we define Tz, the component of the torque about the z axis, to be minus the derivative of the potential energy with respect to the angle of rotation of the body about the z axis,


We have
already identified the momentum conjugate to  as one component, Lz,
of the vector angular momentum
as one component, Lz,
of the vector angular momentum 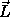 (see section 2.9), so
(see section 2.9), so

Since the orientation of the reference rectangular basis vectors is arbitrary, we may choose them any way that we please. Thus if we want any component of the vector torque, we may choose the z-axis so that we can compute it in this way. We can conclude that the vector torque gives the rate of change of the vector angular momentum

Having obtained a general prescription for the vector torque, we address how the vector torque may be included in Euler's equations. Euler's equations expressed the fact that the vector angular momentum is conserved. Let's return to that calculation, but now include a torque with components T:

Carrying out the same steps as before, we find
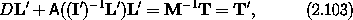
where the components of the vector torque on the principal axes are

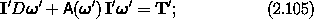

Note that the torque entered only the equations for the body angular momentum or alternately for the body angular velocity vector. The equations that relate the derivative of the orientation to the angular velocity vector are not modified by the torque. In a sense, Euler's equations contain the dynamics, and the equations governing the orientation are kinematic. Of course, Lagrange's equations must be modified by the potential that gives rise to the torques; in this sense Lagrange's equations contain both dynamics and kinematics.
Exercise 2.16. Bicycle wheel
a. Imagine that you are holding a bicycle wheel by the
axle (in both hands) and the wheel is spinning so that the top edge is
going away from your face. If you torque the wheel by pushing down
with your right hand and pulling up with your left hand the wheel will
precess. Which way does it try to turn?
b. A free bicycle wheel rolls on a horizontal surface. If it starts to tilt, the torque from gravity will cause the wheel to turn. Which way will it turn? The reasoning that applied to part a does not directly apply to the rolling bicycle wheel, which is not a holonomic system. However, it is interesting to think about whether the behavior of the two systems is related.
Exercise 2.17. Precession of the equinox
The Earth spins very nearly about the largest moment of inertia, and
the spin axis is tilted by about 23o to the orbit normal.
There is a gravity-gradient torque on the Earth from the Sun that
causes the spin axis of the Earth to precess. Investigate this
precession in the approximation that the orbit of the Earth is
circular and the Earth is axisymmetric. Determine the rate of
precession in terms of the moments of inertia of the Earth.
20 Rotating the cross product of two vectors gives the same
vector as is obtained by taking the cross product of two rotated
vectors: R ( ×
×  ) = (R
) = (R ) × (R
) × (R ).
).
21 In this equation we have a partial derivative with respect
to a component of the coordinate argument of the potential
energy function. The first subscript on the  symbol
indicates the coordinate argument. The second one selects the
symbol
indicates the coordinate argument. The second one selects the
 component.
component.