Dynamic Behavior

Static transfer curves do not address the dynamic behavior of logic circuits. Although the static transfer characteristic of the system was determined by one free parameter, the dynamic characteristics are much more complicated. Even given the constraints on the transfer characteristic of the last section the dynamics depends on choices of $\gamma$, [B₀], k₃, k₄, k₆, and k₇. We have not yet explored this space, so we show here the behavior of only one choice. In the simulations we have chosen the following values for the free parameters--we have not tried to scale these for biologically plausible time scales and concentrations. But similar behavior can be obtained over very wide ranges of variations of these parameters.

$$n=4, \gamma=25, B_0=0.1, k_3=0.2, k_4=0.03, k_6=1.0, k_7=1.5$$

In figure 5 we show behavior of our gates when stimulated with a abrupt transition (square wave) input signal, by turning on and off production of protein A. The concentration of A then changes, as shown in the simulation, due to the sudden production change, in combination with the concentration-dependent destruction rate, and its binding to B_G. The binding of A to DNA inhibits production of B, entailing the changes in the concentration of B, thus yielding the inverter behavior desired.

  

Figure 5: The top trace shows the externally-imposed drive, the rate of production of protein A. The middle trace shows the response of [A]. The bottom trace shows the response of [B]. The two rises of [B] do not look the same because the simulation was started with an arbitrary initial state. Subsequent rises of [B] would look very much like the second one.

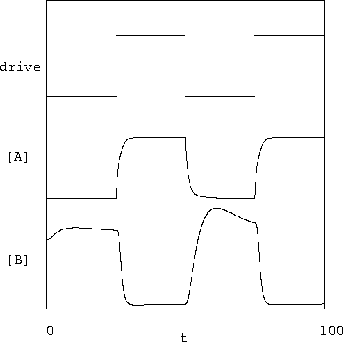Note that the simulation shown in figure 5 the inverter is not loaded by connection to the next stage. We must show that the inverters work with an attached load. One way to do this, which also shows other important features of the dynamics, is to hook three of these inverters up to make a ring oscillator. Simulation of this oscillator (see figure 6) demonstrates that we actually have working inverting amplifiers. In this simulation we started with a random initial condition. We see that our parameters are not particularly optimal, but the system oscillates with reasonable swing.

  

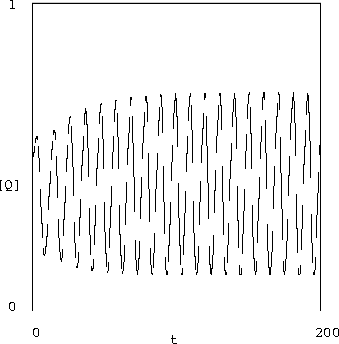Figure 6: The ring oscillator oscillates at a rather high frequency, limited by the rise time, the fall time, and the storage time of the inverter.