Equilibrium Behavior

We need to put further constraints on our concentrations to make a useful inverter. In particular, we want the output of an inverter to be a signal in the same analog range as the input, and we may require the output to go through the halfway point just when the input does. These constraints will restrict the possible values of the parameters $\alpha$ , $\beta$ , $\gamma$ , and [B₀].

Let's start by declaring that the range of signals is the interval [0, 1]. So we require that [A]=0 when [B]=1. This is a free choice, because it just determines the units that we use to measure the concentrations. We can also require that [A]=1/2 when [B]=1/2. This is an actual restriction on our transfer characteristic. Plugging these constraints into the equation (17) results in the relationships:

$\begin{align}\beta &= \gamma [B_0] - 1 \\ \alpha &= 24 \gamma [B_0] - 8 \end{align}$

These leave us with exactly one free parameter for the transfer characteristics of our inverter, $\gamma [B_0]$ . Do we get a good inverter for reasonable values of this parameter? The answer is yes.

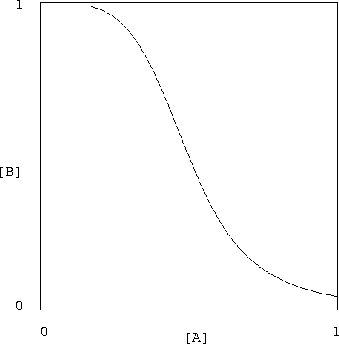
Figure 1 shows that the relationship in equation (17) between the input and output concentrations yields the classic transfer curve of a good digital inverter. (Here n=4and $\gamma [B_0]=2.5$ .) Note, in particular, the low gain for high and low input concentrations, separated by a relatively high-gain transition region. This nonlinearity is the essence of digital gates, and forms the basis for effectively rejecting small variations in the input signals--that is, for attenuating the input noise.

**Figure 1:** The DC transfer curve for our mechanism is similar to the characteristic of an NMOS inverter.
$\begin{figure} {\centerline{\psfig{figure=transfer.ps,width=3in,height=3in,angle=-90}} } \end{figure}$

It is encouraging that the proposed inverter shows promising low sensitivity to variations in the chemical rate constants. The sets of curves shown in figures 2 and 3 display the results of halving and doubling of each of the constants $\alpha$ , $\beta$ in equation (17), while holding $\gamma [B_0]$ constant. Of course, changing these constants violates our constraints (equations (18,19)) but the resulting system is still quite serviceable.

**Figure:** Variation in the parameter $\alpha$ affects the inverter threshold of the gate. Here we see the effect of a factor of four variation in $\alpha$ .
$\begin{figure} {\centerline{\psfig{figure=transfer-a.ps,width=3in,height=3in,angle=-90}} } \end{figure}$

**Figure:** Variation in the parameter $\beta$ affects the concentration representing a logic *one*. Here we see the effect of a factor of four variation in $\beta$ .
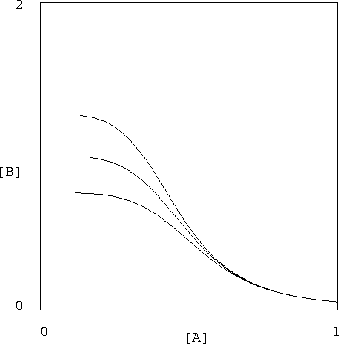$\begin{figure} {\centerline{\psfig{figure=transfer-b.ps,width=3in,height=3in,angle=-90}} } \end{figure}$

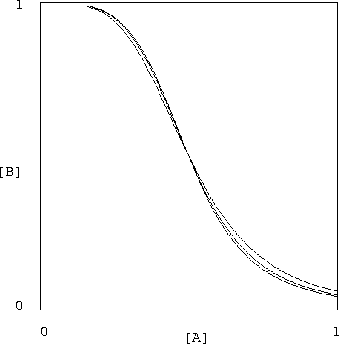
What is even more spectacularly encouraging is that the value of $\gamma [B_0]$ can be varied over a huge range without making this inverter unusable. In figure 4 we see that varying $\gamma [B_0]$ over the entire range [1, 50] has almost no effect on the characteristic shape of our inverter.

**Figure:** Variation in the parameter $\gamma [B_0]$ has almost no effect on the inverter characteristic. Here we vary $\gamma [B_0]$ over a factor of fifty
$\begin{figure} {\centerline{\psfig{figure=transfer-G.ps,width=3in,height=3in,angle=-90}} } \end{figure}$

Of course, this is still useless unless the kinetic constants for biologically feasible reactions are within these ranges. We have not yet done this analysis, but we hope to have results to report shortly.