Homogeneous Coordinates
Notice, how we have snuck up on the idea of Homogeneous Coordinates,
based on simple logical arguments. Keep the following in mind:
coordinates are not geometric,
they are just scales for basis elements. Thus, you should
not be bothered by the fact that our coordinates suddenly have 4 numbers.
We could have had more (no one said we have to have a linearly independent basis set).
Note how this approach to coordinates is completely consistent with our intuitions.
Subtracting two points yields a vector.
Adding a vector to a point produces a point.
If you multiply a vector by a scalar you still get a vector.
And, in most cases, when you scale points you'll get some nonsense 4th
coordinate element that reminds you that the thing you're left with is no longer a point.
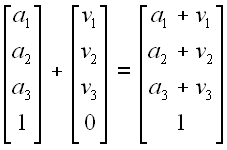
Isn't it strange how seemingly bizarre things
make sense sometimes?
|
|
