Making Sense of Points
There are some operations that do make sense for points.
For instance, if you want to compute a vector that describes the motion from one point to another.
We'd also like to compute one point that is some vector away from a given point.
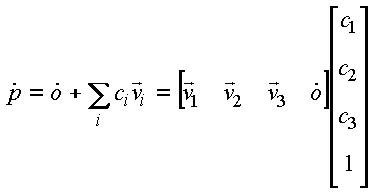
One of the goals of our definitions is to make the subtle distictions between points and vectors apparent.
The key distiction between vectors and points are that points are absolute whereas vectors are relative.
We can capture this notion in our definition of a basis set for points. A vector space is completely defined
by a set of basis vectors, however, the space that points live in requires the specification of an absolute origin.
|
|