Points
Points and vectors are different concepts.
A point is a fixed place in space. A vector can be
thought of as the motion between points. As mentioned
previously, we will distinguish between points and
vectors in our notation.
Points are denoted as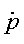 and vectors
as and vectors
as . .
Furthermore, we will consider vectors to live in the
linear space R3 and points to
to live in the Affine space
A3. Let's consider this
distinction.
Conceptually, the operations of addition and
multiplication by a scalar are well defined for
vectors. The addition of 2 vectors expresses the
concatenation of 2 motions. Multiplying a vector by
some factor scales the motion.
However, these operations don't make sense for
points. What should it mean to add to points together?
For example, what is Cambridge plus Boston? What does
it mean to multiply a point by an arbitrary scalar?
What is 7 times Brookline?
|
|
|