If we apply this matrix to coordinates there must be some implied basis,
because coordinates alone are not geometric entities
(a basis is required to convert coordinates into a vector).
Assume this implied basis is .
Thus, our coordinates describe the vector .
Thus, our coordinates describe the vector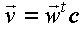 .
The resulting transform, .
The resulting transform,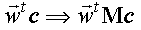 , will
stretch this vector by a factor of 2 in the direction of the first element of the basis set. Of course that direction
depends entirely on , will
stretch this vector by a factor of 2 in the direction of the first element of the basis set. Of course that direction
depends entirely on . .
|
These illustrations show the significance of the basis when transforming vectors.
(Click on the images below)
|