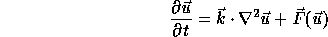
Turing suggested that the mechanisms of morphogenesis can be explained by ``reaction-diffusion'' equations (see [11]). These are systems of partial differential equations of the form
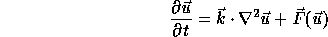
where the vector-valued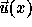 
at each time t describes the
changing spatial concentrations of a set of chemical substances called
``morphogens''. The resulting Turing patterns for various
reaction specifications 
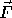have been widely simulated and have
been shown to produce regular patterns reminiscent of zebra stripes
and leopard spots. Whether or not reaction-diffusion mechanisms are
the actual phenomena in such biological systems,
simulation of such systems does tend to generate regular patterns that
appear as standing-wave solutions to the equations.
Interestingly, the resulting Turing patterns are often independent
of the initial state of the system. Starting from a random
configuration and evolving the equation eventually results in regular
patterns in the concentrations of the morphogens.
Figure 2 shows one such set of patterns,
obtained from a random initial distribution in a system
that evolves according to a system of reaction-diffusion equations called the
Gray-Scott model. We have built a simulation environment for
exploring these kinds of reaction models. Figure 2
shows a sample result.
Figure 2:
Simulation of the Gray-Scott model starting from a random initial
configuration (left) and evolving to regular spots after 20,000 time
steps (right). There are 2500 particles randomly packed in a square
of size 1, starting with values of the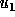 
and
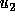morphogens randomly assigned between 0 and 1. Each particle's neighbors are those
within a distance of 0.05 from it. The constants for the Gray-Scott
model here are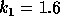 
, 
, 
, 
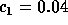, and
integration is performed using the forward-Euler method with 
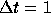. The different colors of the particles indicate different values
of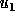 
.
This suggests the intriguing possibility of organizing amorphous computing systems by starting with the particles in a random state and solving a discrete analog of a reaction-diffusion system. The resulting regularly spaced ``blobs'' of particles could then serve as organizing centers for subsequent stages of computing.