Suppose we paint a surface with smart paint: We want the paint to divide the surface into a few labeled regions, to identify the boundaries between regions, and to generate a global data structure that reflects the topology of how the regions are connected. This region definition problem might be the first step in a program that monitors the integrity of the structure that the paint covers, or performs distributed control based on observing the local dynamical variables.
In our imagined paint, there are enough computational elements that we may think of them as particles that are randomly and uniformly distributed throughout the paint. Each particle can communicate with ten or twenty nearby neighbors, for example, through very short-range radio or electrostatic communication, but a particle does not know the directions or distances to its neighbors. (This is a conservative assumption. Some hardware substrates may provide more geometric information than this.) Each particle also has a hardware random-number generator (not pseudo-random) that it can use to choose an almost-unique identifier (the ID). We do not assume that there is any a priori synchronization among particles.
To accomplish region definition, suppose that we are already at the point where each particle has identified a set of neighbors with which it can communicate. (Identifying the neighbors is already a complicated part of the bootstrap process, but we will not talk about it here.)
The first step is to do some small-scale local clustering. Each particle initializes a state variable (its LOWNUM) to be that particle's ID. The particle compares its LOWNUM to those of its neighbors and adopts the smallest value as its new LOWNUM. This process continues for a few iterations. At the end of this step we have a few regions (particles that all have the same LOWNUM). Each region has a radius approximately equal to the number of iterations, but the regions are raggedly shaped, and they may have holes and ill-defined boundaries.
The next step is to regularize the regions: smooth the edges and fill in the holes. This can be done with a peer pressure algorithm. Each particle computes a frequency table of the LOWNUMs of itself and its neighbors, finds the LOWNUM that is asserted most often, and adopts this as its new LOWNUM. This process continues until things stabilize. Note that the LOWNUM for a region is in fact the particle ID of a particular particle in that region. We can choose that particle to act as a representative for the region. (Figure 1 shows an example of the algorithm in progress.)
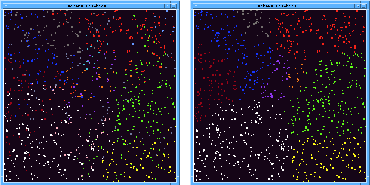
Figure 1: Progress of the region-growing
algorithm, from an initial configuration of 1000 particles placed at
random in a square of edge 1. Each particle's neighbors are all the
particles within a distance of of 0.1 from it. The picture on the
left shows the regions formed after local clustering but before
regularization. The figure on the right shows the effect of
regularization. Before regularization there are many regions and the
various regions are mixed together. Note how the regions become
compact and well-defined when regularized.
At this point the particles know whether they are interior to a region, or on the boundaries between regions: Each particle notes all the LOWNUMs asserted in its neighborhood. A particle that sees more than one LOWNUM is near an edge. Particles that see exactly two LOWNUMs are interior to the edge. More than two LOWNUMs signals a vertex.
Now we use the same LOWNUM propagation algorithm, but restricted to edges, so that each edge adopts a representative ID (and associated particle). Each edge propagates to only those edges that have the same two regions that they bound. Thus, disjoint edges that bound the same two regions will be given different identifiers.
Now we do the same process for vertices, the particles at each vertex pick an ID for the vertex (and a corresponding representative particle).
Finally, we combine all this information by broadcast accumulation. Each particle broadcasts what it knows: the IDs of the regions, edges, and vertices, which edges separate which regions, and which edges meet at each vertex. Initially, a particle knows only about the structures it is a part of. But, as a particle receives more information, it passes this along. To prevent saturation of communication, a particle passes information along only when it learns something new. Eventually, all particles will know all the information.
This example is instructive in several ways:
