


Next: Example: Using approximate
Up: Getting started: Programming
Previous: Example: Region definition
Many physical processes, such as the flow of air over a wing or the
vibration of a membrane, are described in terms of fields constrained
by partial differential equations (PDEs). Mechanisms that depend on
controlling such systems may have to solve these equations, at least
approximately, in real time. This kind of computation is currently
very costly and requires large computational resources, which, for
example, are not easily integrated into an airplane wing. An
amorphous computer incorporating the sensors and actuators, integrated
into the system to be measured and controlled, may be exactly what is
required for this computationally demanding but highly local activity.
We can start to investigate this kind of computation by examining some
elementary autonomous partial differential equations to see what it
takes to compute their solutions by an intelligent material. Suppose
we use each computational particle to represent a region of space (or
space-time). If the computational particles actually know their
positions accurately, then good methods are available to approximate
the differential operators to high order, even though the neighbors
are not related by a regular grid. But, unless they are the sources
of physical measurements or the controls of physical actuators, it is
not really necessary that the assumed positions of the particles are
their actual positions. In fact, all that matters is that there is a
consistent set of positions assigned to the processors (so that
processors that think that they are near each other in the simulated
space can communicate efficiently).
We shall show in the next section how one might arrange for particles
to choose appropriate consistent positions for high-accuracy
computations. However, even if the particles have no information
about their positions, it still is possible to compute a low-accuracy
solution to some PDEs, using an amorphous process that approximates
the spatial locality of the formulation of the PDE with the local
communication available to the particles.
One such PDE is Laplace's equation, 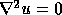 , whose solutions are
the harmonic functions. For any solution of Laplace's equation, each
interior point is the average of the points around it. On a regular
grid this yields a good approximation method that can be relaxed to
get accurate solutions. However, even on a random grid, where there
is no information about the distance or direction to each neighbor,
our preliminary analysis and simulations shows that the process of
replacing every point's value with the average of its communicating
neighbors converges to an approximation to a solution of Laplace's
equation. We need only set up appropriate boundary conditions to
approximate a designated harmonic function.
, whose solutions are
the harmonic functions. For any solution of Laplace's equation, each
interior point is the average of the points around it. On a regular
grid this yields a good approximation method that can be relaxed to
get accurate solutions. However, even on a random grid, where there
is no information about the distance or direction to each neighbor,
our preliminary analysis and simulations shows that the process of
replacing every point's value with the average of its communicating
neighbors converges to an approximation to a solution of Laplace's
equation. We need only set up appropriate boundary conditions to
approximate a designated harmonic function.



Next: Example: Using approximate
Up: Getting started: Programming
Previous: Example: Region definition
Gerald Jay Sussman
Thu Jun 27 16:56:19 EDT 1996
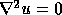 , whose solutions are
the harmonic functions. For any solution of Laplace's equation, each
interior point is the average of the points around it. On a regular
grid this yields a good approximation method that can be relaxed to
get accurate solutions. However, even on a random grid, where there
is no information about the distance or direction to each neighbor,
our preliminary analysis and simulations shows that the process of
replacing every point's value with the average of its communicating
neighbors converges to an approximation to a solution of Laplace's
equation. We need only set up appropriate boundary conditions to
approximate a designated harmonic function.
, whose solutions are
the harmonic functions. For any solution of Laplace's equation, each
interior point is the average of the points around it. On a regular
grid this yields a good approximation method that can be relaxed to
get accurate solutions. However, even on a random grid, where there
is no information about the distance or direction to each neighbor,
our preliminary analysis and simulations shows that the process of
replacing every point's value with the average of its communicating
neighbors converges to an approximation to a solution of Laplace's
equation. We need only set up appropriate boundary conditions to
approximate a designated harmonic function.


