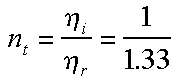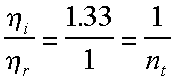Project 5

Project 4 in case you need it.

Objective

In this last project you are asked to make some extensions to the ray tracer given in class. In particular, you should add refraction to the illumination model, finish adding triangle meshes, and add a cylinder and/or cone primitive. Ray Tracing is one of the easiest ways of generating visually stunning pictures.

Checkpoint (Due Wednesday November 28 at 8pm)

• The last two parameters of the surface model k_t and n_t should be interpreted as follows; k_t is the fraction of the transmitted ray's intensity that is reflected to the eye, n_t is the ratio of the surrounding material's index of refraction to the object's index of refraction. For example, if you want to simulate a spherical water drop the index of refraction for water is approximately 1.33 (glass is approximately 1.5). If we assume the surrounding material is air then its index of refraction is 1. So when a ray strikes the outside of the object the term used in the equation given in class is computed as follows.
  
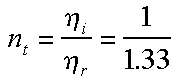
  And when a ray inside of an object exits it then the term used in the equations is computed as follows.
  
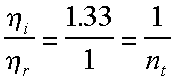
• The Ray class should be extended to keep track of whether the ray is entering or exiting the object at an intersection. This info needs to be passed to the Surface shader so it knows whether to use n_t or its inverse. We assume that transparent objects won't intersect and so transitions are always from air or into air.
• Consider what happens when the ray starts inside of a sphere (as it will in this project). Will the sphere intersection code still work?
• Note that the raytracer as currently written will continue tracing rays forever until one fails to run into something. What's going to happen inside a transparent sphere? Or, if you put two mirrors in front of each other? Maybe you should limit the depth of the Ray tree to some fixed maximum depth, e.g. 10.
• You might want to speed up the shadow test, which currently tests every object for each shadow ray, even after it has found an intersection. Does it make a difference?
• What does a crystal ball look like?
  
  
  Your mileage may vary...

Project5 (Due Wednesday December 5 at 8pm)

1. Finish coding the Triangle intersect and Shade methods in Triangle.java. Test the results with one of the test cases involving polygon meshes, show us the cow test case.
2. Add your own primitive. For example, one of:
   • cone tipX tipY tipZ baseX baseY baseZ baseRadius
   • cylinder topX topY topZ baseX baseY baseZ Radius

Extra Credit

• Add more primitives, e.g. torus.
• Add texture mapping, e.g. create a Raster from an image and map it onto the surface of a sphere.
• Add bump mapping.
• Incorporate bounding volumes or spatial subdivision

Files

• RayTrace.java This is the top-level of the ray tracer.
• RayTraceApplet.java Code for the applet that calls the ray tracer.
• Light.java The Light class.
• Surface.java The Surface class, contains the critical Shade method. You need to add refraction here.
• Ray.java The Ray class.
• Renderable.java The Renderable interface.
• Sphere.java The Sphere class, check the intersect method.
• Triangle.java The Triangle class, complete the intersect and Shade methods.
• TriangleMesh.java The TriangleMesh class.
• Vector3D.java The Vector3D class, with methods for common vector operations.
• balls.ray Input file with reflective spheres.
• sboard.ray Input file with transparent sphere and a "checkerboard" made of spheres.
• cow.ray The purple cow on a reflective surface.
• test.ray A small triangle mesh and a transparent sphere. May be useful for debugging.

Ground Rules

• Feel free to discuss assignments and your approach with others.
• Don't use code from previous semesters.
• The design and code must be your own.
• Cite any models, images, ideas, or algorithms that you do not develop yourself.
• The assignment and the checkpoint are due before 8pm of the days indicated.
• A working version of your applet and source code must be linked to your course home page.
• All source code must also be submitted via Athena's turnin procedure.
  1. Develop your projects in directories named project1, project2, etc. (depending on the project number)
  2. Before turning in, put your project in a tar archive using tar command on athena:

     tar -cvf projectX.tar projectX

     • here projectX.tar is the archive name, and projectX is your project directory.
     • X is the project number.
     • make sure you are in the parent directory of projectX
  3. Use turnin command to turn in the tar file

     turnin -c 6.837 X projectX.tar

     Make sure you include the course number (-c 6.837) and the project number (X).
  4. For example, to turn in project 5:
     • make sure your project is in the directory named 'project4'
     • go to the parent directory of project5
     • type 'tar -cvf project5.tar project5' to create the tar archive
     • type 'turnin -c 6.837 5 project5.tar' to turn in the archive
  5. Check this page frequently for updates and clarifications.