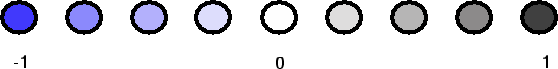Next: About this document ...
Up: Discrete, Amorphous Physical Models
Previous: Bibliography
Figure:
An example of an irregular lattice in two dimensions.
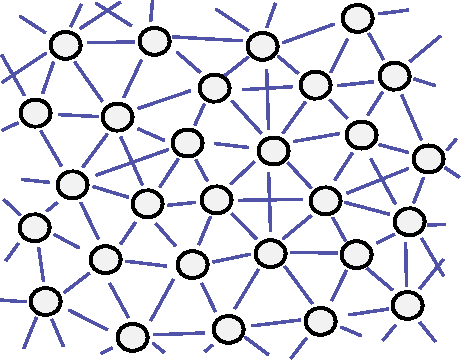 |
Figure:
A cluster of sites.
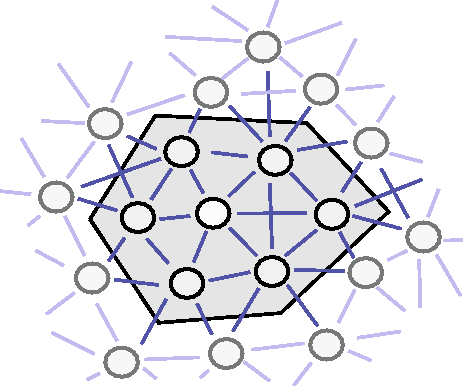 |
Figure:
A ``box'' enclosing a pair of neighbors.
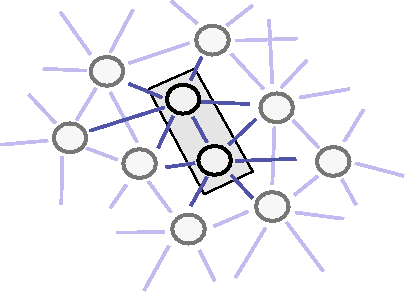 |
Figure:
Two neighboring sites exert a ``force'' on each other as if
they were masses connected by springs. Each mass is free to move in
one dimension.
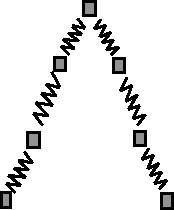 |
Figure:
Two-dimensional evolution of diffusion model. a=0.05,
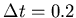 .
.
|
Figure:
Superposition. a=0.05,
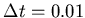 ,
k = 1,
neighborhood size variance = .0384. Sites are equally spaced but have
variable sized neighborhoods. Above, the pulse is shown splitting into
left-travelling and right-travelling pulses. Below, the pulses are
shown after they have wrapped around the periodic boundary conditions
and passed through each other twice, four times, and six times.
,
k = 1,
neighborhood size variance = .0384. Sites are equally spaced but have
variable sized neighborhoods. Above, the pulse is shown splitting into
left-travelling and right-travelling pulses. Below, the pulses are
shown after they have wrapped around the periodic boundary conditions
and passed through each other twice, four times, and six times.
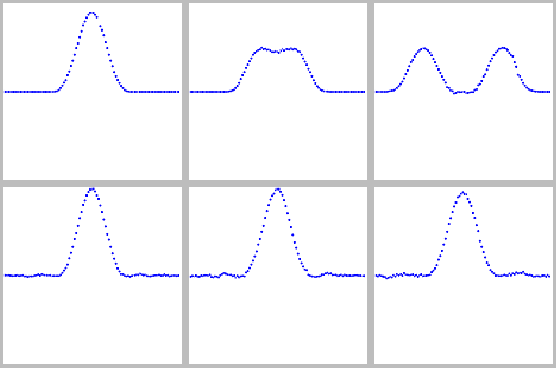 |
Figure:
A momentum wave in the energy-conserving wave model. The
initial conditions are a pulse as in figure 6,
and parameters are the same. There are 101 regularly spaced
sites. Momentum rather than position is shown. The first four frame
show the pulse in the process of splitting; the last shows it after
one period. Energy was calculated to be identical before, during, and
after the sequence, with a value of 0.33980601.
 |
Figure:
Colors used in illustrations. Shades indicate amplitude from
blue (-1) through white (0) to black (1).
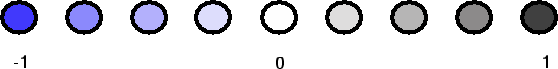 |
Figure:
Two-dimensional evolution of wave model. a=0.05,
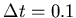 ,
k = 1.
,
k = 1.
 |
Figure:
Reflection. There is a parabola-shaped fixed boundary at
right. The initial condition is a line wave, which becomes focused to
a point in the third frame.
 |
Figure:
Refraction. The central region has twice the density of
sites as the rest of the space, but the neighborhood size remains
about the same.
 |
Figure:
Snapshot of amplitudes. As in Fig. 9 but with
periodic boundary conditions.
 |
Figure:
Standing wave, comparison with exact solution. There are
101 processors arranged regularly in one dimension with two neighbors
each; the graph shows the amplitude of the processor closest to the
center plotted against average number of transactions per processor,
versus the exact solution of the wave equation,
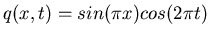 ,
with initial conditions
,
with initial conditions
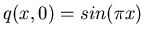 .
a=0.05,
.
a=0.05,
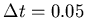 ,
k = 1.
,
k = 1.
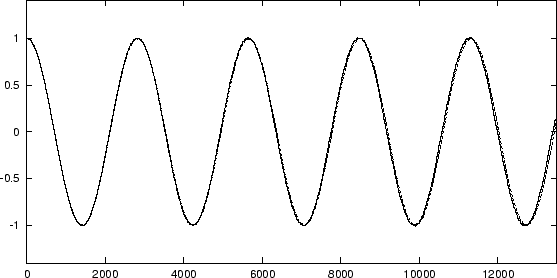 |
Figure:
Comparison with solution of PDE: D(t) with exact solution
over time for different levels of asynchrony a. The x-axis
represents the average number of transactions per processor.
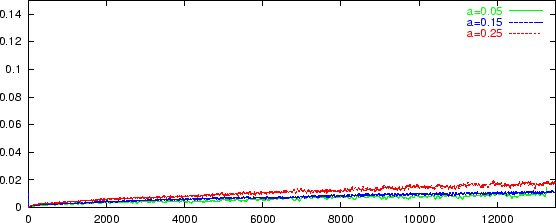 |
Figure:
Pulse, comparison D(t) with PDE solution. The sites are
in one dimension with variable sized neighborhoods; the variance in
neighborhood size is .0384. D(t) is plotted for regular and irregular
geometry with 101 sites, and irregular geometry with 201 sites. In the
first two, the pulse completed about two periods while in the last, it
completed one period (a period being the time it takes the two halves
of the pulse to wrap around the boundaries to their original starting
points). a=0.05,
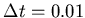 ,
k = 1. The effect of
irregularity is compensated for by using a greater density of sites.
,
k = 1. The effect of
irregularity is compensated for by using a greater density of sites.
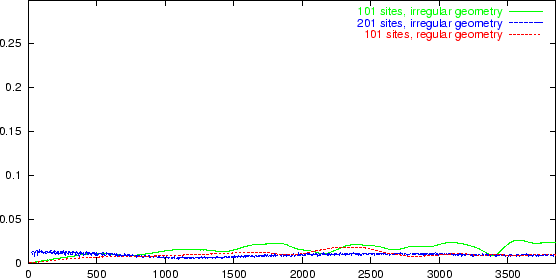 |
Figure:
As above, but normalized so that exactly two periods are
completed in each case. The x-axis here represents periods.
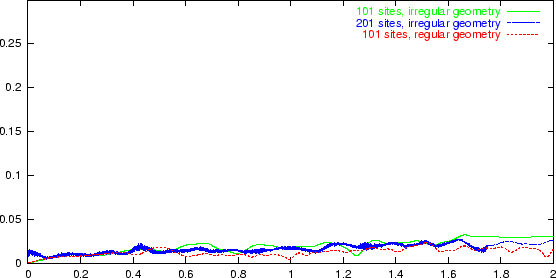 |
Figure:
Comparison with PDE solution Dp(t) for the momentum wave.
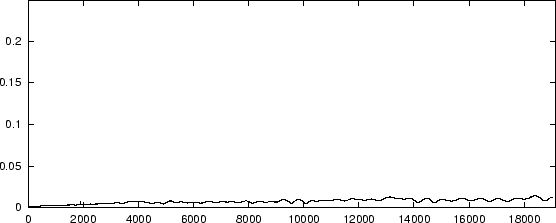 |



Next: About this document ...
Up: Discrete, Amorphous Physical Models
Previous: Bibliography
Erik Rauch
1999-06-26