MASSACHVSETTS INSTITVTE OF TECHNOLOGY
Department of Electrical Engineering and Computer Science

6.002x - Circuits and Electronics
Spring 2004

BJT's Without Tears¹

Transistor circuits can be daunting for beginning students. It's a big jump in complexity beyond resistors. Some reasons are:

• Resistors are two-terminal devices, and we generally work in terms of only two variables: $v$ and $i$. Transistors are three-terminal devices, and we use six variables: $i_{\sc c}$, $i_{\sc b}$, $i_{\sc e}$, $v_{\sc be}$, $v_{\sc cb}$, $v_{\sc ce}$.

• For resistors, there's a single equation $v=Ri$ to consider. For transistors, you use different equations and make different assumptions, depending on the way the transistor is operating.

• The simple resistor equation is a (surprisingly) accurate physical model. The transistor models are relatively crude approximations, and there are a series of more and more complex models that take more and more factors into account.

When faced with a transistor circuit, how do you decide which equations to use and which assumptions to make. The most general answer is (maddeningly)--``it depends''.

Fortunately for you, the circuits we'll be asking you to work with in 6.002x are artifacts that were designed for a purpose rather than arbitrary bunches of components that happen to be connected together. You can therefore get a hint of how the transistor is operating by making a guess about the intent of the circuit. In addition, since the circuit was designed, the operation of the transistor is will probably be satisfactorily described by a simple model: otherwise the person who designed the circuit wouldn't have understood it enough to design it!²

This note presents a procedure for analyzing circuits with bipolar junction transistors. It's not foolproof, but it's good enough for 6.002x (and much else).

Here's the general form of the procedure:

1. Guess how the transistor is operating, based on what you think the circut is supposed to be doing. The model of operation will include equations that relate the circuit quantities, and it will specify constraints that must hold in order for the model to be applicable.

2. Using the equations for that model, do circuit analysis to check that the applicability constraints are satisfied. If they are, then your calculations using the model will give useful information about the circuit. If not, try again with a different model.

Now for the details ...

Transistor symbols

Figure 1: NPN and PNP bipolar junction transistor symbols, showing standard reference directions for the currents and voltages.

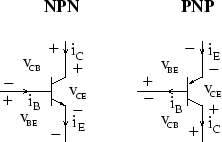Figure 1 shows the standard symbols for NPN and PNP bipolar junction transistors. The small solid arrow on each symbol identifies the emitter. The arrow faces out to indicate an NPN transistor and in to indicate a PNP transistor. Observe the open arrows indicating the reference directions for the currents: For an NPN they flow in to the base and the collector, and out from the emitter. For a PNP they flow out of the base and the collector, and into the emitter. We've drawn the NPN transistor with the emitter on the bottom, and the PNP transistor with the emitter on the top, so that in both cases the reference direction for current flow is ``down'' as seen on the page. This is a common convention, but watch out for circuits with transistors that are ``upside down''.³

For either kind of transistor, and for any of the models you'll use below, it is always true that $i_{\sc e} = i_{\sc b} + i_{\sc c}$ and $v_{\sc ce} = v_{\sc cb} + v_{\sc be}$, since these are just KCL and KVL for a three-terminal device.

NPN transistors

Suppose you need to analyze a circuit that contains an NPN transistor.

Try analyzing the transistor as a switch

For almost all circuits you'll encounter, the transistor is acting either as a switch or as an amplifier.

Do you think the transistor is being used as a switch? If so, it should be operating either in the cutoff region or in the switched-on region, depending on the inputs and on the region of operation of the other transistors in the circuit.

Step 1: Check that the transistor can be cutoff:

For cutoff we have $i_{\sc e}=i_{\sc b}=i_{\sc c}=0$ and $v_{\sc be}<0.7~{\rm Volts}$. To check for cutoff, analyze the circuit assuming that the currents are zero. If the base voltage that you obtain is more than 0.7 Volts then the assumption was false and the transistor is not cutoff.

Step 2: Check that the transistor can be switched-on

For the switched-on region we have $i_{\sc c} > 0$, and $v_{\sc ce}<0.2$. To verify that the transistor is switched-on, show that $i_{\sc c} > 0$, and $v_{\sc ce}<0.2$ is consistent with the expected operating conditions.

Try analyzing the transistor as an amplifier

Do you think the transistor is being used as an amplifier? If so, it should be operating in the amplification region.

Step 1: Check for cutoff:

See whether the transisitor is cutoff (as above). If it is, then this is probably not an amplifier circuit, or at least not a good one.⁴ Check whether the transistor is really intended to be used as a switch. If it's not a switch, then go to part 2.2.1.

Step 2: Is the emitter just following the base?

If a transistor is operating in the amplification region then it is often very easy to get a good estimate of the behavior by assuming that the emitter voltage is following the base: $v_{\sc be}=0.7~{\rm Volts}$. A further simplification that is often useful is the assumption that $\beta$ is infinite, which implies that $i_{\sc b}=0$ and $i_{\sc c}=i_{\sc e}$.

Step 2a: Eyeball Test:

Examine the circuit to try to spot whether it makes sense to use this follower model. For example, if the emitter voltage is pinned (by the rest of the circuit) while the base voltage moves, then the transistor's behavior can't be understood this way. If the circuit fails the eyeball test, go to step 3.

Step 2b: Amplification region test:

If the circuit passes the eyeball test, do analysis to check whether $v_{\sc ce}>0.2$ (i.e., the transistor remains in the amplification region) for expected operating conditions. In general, this analysis will depend on the entire circuit. If $v_{\sc ce}<0.2$, the tests fails: go to step 3. During this analysis you will obtain a collector current, which will be useful in step 2c.

Step 2c: Fix the infinite $\beta$ assumption:

If you previously used the simplifying assumption that $\beta=\infty$ then we now have to make sure that this did not invalidate the deductions. Assume $\beta$ is 100, which is typical for small-signal transistors⁵. Using $i_{\sc c}=\beta i_{\sc b}$ get an estimate of the base current, given the collector current you previously computed. Did this base current change the base voltage enough (for example, by loading a voltage divider) to drive the transistor into cutoff or into the switched-on region? If not, your analysis based on the infinite $\beta$ assumption is useful for understanding the circuit. Otherwise go on to step 3.

Step 3: Try the exponential model

If the follower model doesn't work, then you can't assume that $v_{\sc be}$ remains fixed at 0.7 Volts. Assume again that $\beta$ is infinite, so so $i_{\sc b}=0$ and $i_{\sc c}=i_{\sc e}$. Assume that $i_{\sc e}$ and $v_{\sc be}$ are related by

$$i_{\sc e} = I_0 (e^{\frac{q}{kT} v_{\sc be}} - 1) ,$$

where $q/kT$ is 38 and $I_0$ is $10^{-14}$, which are typical values.⁶

Using these values, try the amplification region test (step 2b above) and the $\beta$ test (step 2c). If they work, then this exponential model was appropriate for analyzing the circuit.

Cry

If neither of the amplifier models work, and the transistor isn't operating as a switch, the either the transistor is intended to be an amplifier and really does become cut off or switched on (maybe the circuit doesn't work or maybe it was really designed to take advantage of this in some fiendish way) or you need to apply a more complicated model of the transistor, which we won't be doing in 6.002x.⁷

A note on circuits with several transistors:

If the circuit has several transistors that all interact, this process can get extremely complicated because you have to consider the different possible regions for each transistor. So hope that the circuit is designed so that the transistors can be considered independently.

PNP transistors

PNP transistors behave exactly the same as NPN transistors, except for a few signs. Using the labeling conventions we show in figure 1 $i_{\sc c}=\beta i_{\sc b}$ as before, and only the signs of the voltages are changed.

The PNP transistor turns on at $v_{\sc be} = -0.7~{\rm Volts}$ and it switches on if $v_{\sc ce} > -0.2~{\rm Volts}$, and the equation describing the behavior of the transistor in the amplification region is:

$$i_{\sc e} = I_0 (e^{-\frac{q}{kT} v_{\sc be}} - 1) .$$

Why?

The analysis techniques described outlined here are a distillation of years of experience. When analyzing an amplifier we try to use the 0.7 Volt infinite $\beta$ model first because if it is appropriate the amount of work we have to do is very small. We should never depend on the $\beta$ of a transistor being any particular value, because this parameter is highly variable, both by sample and by temperature.

On the other hand, the 0.7 Volt drop for a transistor operating in the amplification region is a pretty good representation of the transistor to the rest of the circuit. However, never use the 0.7 Volt assumption with the exponential equation. The collector current computed this way is very sensitive to errors in the base-emitter voltage, so the result will be meaningless. But it is OK to use the infinite $\beta$ assumption with the exponential equation.

A Terminology disaster

To add insult to injury for the student trying to learn about transistors, there is an inconsistent use of terminology describing the regions of transistor operation. Most treatment talk in terms of the transistor's saturation region. Unfortunately, ``saturation'' is usually used to describe different non-analogous regions of operation for Bipolar Junction Transistors and Field Effect Transistors (which you will see soon).

In an attempt to be more consistent, we have chosen in 6.002x to use the words ``cutoff region,'' ``amplification region,'' and ``switched-on region'' to describe the three regimes of operation of a transistor, in a way that is the same for both BJTs and FETs.

However, this requires a mapping to the terminology used in the books we reference:

6.002x	BJT	cutoff	amplification	switched-on
6.002x	FET	cutoff	amplification	switched-on
Senturia & Wedlock	BJT	cutoff	active gain	saturated
Senturia & Wedlock	FET	cutoff	active gain	saturated
Horowitz & Hill	BJT	cutoff	active linear	saturated
Horowitz & Hill	FET	cutoff	saturation	linear
Gray & Meyer	BJT	cutoff	forward active	saturated
Gray & Meyer	FET	cutoff	saturation	ohmic or triode
Agarwal & Lang	BJT	cutoff	active	saturated
Agarwal & Lang	FET	cutoff	saturated	triode

Note in particular that in Agarwal and Lang, ``saturated'' for a MOSFET is the region where you use it as an amplifier, while ``saturated'' for a BJT is the region where you don't use it as an amplifier.

A simple incremental model

Once we have determined the operating point (the DC bias conditions) for a transistor in the amplification region we may want to understand its behavior as a small-signal amplifier. This is accomplished by building an incremental model of the circuit, with the transistor replaced by an incremental transistor model. An incremental model is linear, so it is easy to work with, and it can accurately capture the behavior in terms of small deviations of the voltages and currents.

One useful incremental model for the transistor is as a resistor and voltage-controlled current source (see Figure 2). The parameters of this model are easy to compute. Given the collector bias current $I_{\sc c}$, the transconductance, $g_m$, is $g_m=\frac{q}{kT} I_{\sc c} \approx 38 I_{\sc c}$. The base-emitter incremental resistance $r_\pi$ is computed from $g_m r_\pi = \beta$. If we are working under the assumption that $\beta=\infty$ then we just set $r_\pi=\infty$.

Figure 2: A simple incremental model of an NPN transistor uses a linear voltage-controlled current source to capture the fact that small changes in the voltage from base to emitter of the transistor produce proportional changes in the collector current. The model for PNP is the same, except for the signs.

About this document ...

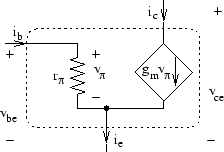This document was generated using the LaTeX2HTML translator Version 2K.1beta (1.48)

Copyright © 1993, 1994, 1995, 1996, Nikos Drakos, Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999, Ross Moore, Mathematics Department, Macquarie University, Sydney.

The command line arguments were:
latex2html bjts-without-tears

The translation was initiated by Hal Abelson on 2004-02-11