MASSACHVSETTS INSTITVTE OF TECHNOLOGY
Department of Electrical Engineering and Computer Science
6.001--Structure and Interpretation of Computer Programs
Spring Semester, 1997
Problem Set 4
A Graphics Design Language
Issued: Tuesday, February 25, 1997
Due: In recitation on Wednesday, March 5 for recitations held at
9, 12, 1 and 2;
and on Friday, March 7 for recitations held at 10 and 11.
Tutorial Preparation: For the week of March 3.
Reading Assignment: Through the end of Section 2.3 of SICP.
In this assignment, you will work with Peter Henderson's ``square-limit'' graphics design language, which will be described in lecture on February 27, and which appears in the text. Before beginning work on this programming assignment, you should review that section. The goal of this problem set is to reinforce ideas about data abstraction and higher-order procedures, and to emphasize the expressive power that derives from appropriate primitives, means of combination, and means of abstraction.
Figure belongs here but could not convert from postscript
Section 1 of this handout reviews the language, similar to what appears in the text. You will need to study this in order to prepare the tutorial presentations in section 2. Section 3 gives the lab assignment, which includes an optional design contest.
Recall that the key idea in the square-limit language is to use painter procedures that take frames as inputs and paint images that are scaled to fit the frames. To do this, we will need some basic building blocks.
Each vector consists of a pair of numbers, glued together in some appropriate manner. The contract we enforce for this data abstraction is the following:
, by which we mean that the procedure takes
two numbers as arguments, and returns a vector object.
, meaning it
takes a vector object as input and returns a number as its value.
We need a set of operations on vectors, and in particular assume three:
which implies that the operation is going to be
closed over the set of vectors);
A pair of vectors determines a directed line segment--the segment running from the endpoint of the first vector to the endpoint of the second vector. Again, we just need a contract:
A frame is represented by three vectors: an origin and two edge vectors.
(define (make-frame origin edge1 edge2) (list origin edge1 edge2))(define origin-frame car) (define edge1-frame cadr) (define edge2-frame caddr)
Thus, make-frame is of type: 
. Each selector is of type: 
.
The frame's origin is given as a vector with respect to the origin of the graphics-window coordinate system. The edge vectors specify the offsets of the corners of the frame from the origin of the frame. If the edges are perpendicular, the frame will be a rectangle; otherwise it will be a more general parallelogram. Figure 2 shows a frame and its associated vectors.
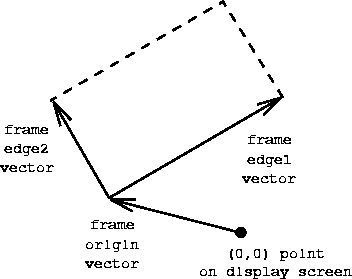
Figure: A frame is described by three vectors--an
origin and two edges.
Each frame determines a system of ``frame coordinates'' (x,y) where (0,0) is the origin of the frame, x represents the displacement along the first edge (as a fraction of the length of the edge) and y is the displacement along the second edge. For example, the origin of the frame has frame coordinates (0,0) and the vertex diagonally opposite the origin has frame coordinates (1,1).
Another way to express this idea is to say that there is a frame coordinate map associated with each frame that takes vectors expressed in terms of the coordinate system defined by that frame, and returns the same vectors, expressed in terms of the original or underlying coordinate system. That is, (x,y) gets mapped onto the underlying coordinates of the point given by the vector sum
We can obtain a procedure which computes the frame coordinate map of a
frame by applying make-frame-coordinate-map of type 
(which means it takes a frame as
argument and returns a procedure which maps vectors to vectors):
(define (make-frame-coordinate-map frame)
(lambda (point-in-frame-coords)
(add-vect
(origin-frame frame)
(add-vect (scale-vect (xcor-vect point-in-frame-coords)
(edge1-frame frame))
(scale-vect (ycor-vect point-in-frame-coords)
(edge2-frame frame))))))
For example, ((make-frame-coordinate-map a-frame) (make-vect 0 0)) will return the same value as (origin-frame a-frame).
The procedure make-relative-frame provides a convenient way to
transform frames. Given three points origin,
corner1, and corner2 (expressed in frame coordinates), it
returns a procedure which for any frame f returns a new frame g
which uses those points in f coordinates to define the corners of
the g frame (this procedure thus has type 
):
(define (make-relative-frame origin corner1 corner2) (lambda (frame) (let ((m (make-frame-coordinate-map frame))) (let ((new-origin (m origin))) (make-frame new-origin (sub-vect (m corner1) new-origin) (sub-vect (m corner2) new-origin))))))
For example,
(make-relative-frame (make-vect .5 .5) (make-vect 1 .5) (make-vect .5 1))
returns a procedure that takes a frame f and returns the upper right quarter of f as a new frame g.
As described in the notes, a painter is a procedure that, given a frame
as argument, ``paints'' a picture in the frame. That is to say, if
p is a painter and f is a frame, then evaluating (p
f) will cause an image to appear in the frame. The image will be
scaled and stretched to fit the frame. Denoting the type of this
procedure is a bit awkward since the result of using a painter is to
cause a picture to appear, rather than returning a specific object.
For notational convenience, we will say that a painter is of type
by which we mean that a painter takes
a frame as input, and returns a set of points, represented as
vectors, that are actually drawn in the frame.
The language you will be working with includes four ways to create primitive painters.
The simplest painters are created with number->painter, which takes a number as argument. These painters fill a frame with a solid shade of gray. The number specifies a gray level: 0 is black, 255 is white, and numbers in between are increasingly lighter shades of gray. Here are some examples:
(define black (number->painter 0)) (define white (number->painter 255)) (define gray (number->painter 150))
You can also specify a painter using procedure->painter, which takes a procedure as argument. The procedure determines a gray level (0 to 255) as a function of (x,y) position, for example:
(define diagonal-shading (procedure->painter (lambda (x y) (* 100 (+ x y)))))
The x and y coordinates run from 0 to 1 and specify the fraction
that each point is offset from the frame's origin along the frame's
edges. Thus, the frame is filled out by
the set of points (x,y) such that 
.
A third kind of painter is created by segments->painter, which takes a list of line segments as argument. This paints the line drawing specified by the list segments. The (x,y) coordinates of the line segments are specified as above. For example, you can make the ``Z'' shape shown in figure 3 as
(define mark-of-zorro (let ((v1 (make-vect .1 .9)) (v2 (make-vect .8 .9)) (v3 (make-vect .1 .2)) (v4 (make-vect .9 .3))) (segments->painter (list (make-segment v1 v2) (make-segment v2 v3) (make-segment v3 v4)))))
The final way to create a primitive painter is from a stored image.
The procedure image->painter uses an image from the 6001 image
collection to create a painter
.
For instance:
(define fovnder (image->painter "fovnder"))
will paint an image of William Barton Rogers, the FOVNDER of MIT.
Figure here unable to convert from postscript
Examples of primitive painters: mark-of-zorro and fovnder.
Given a painter, we can produce a new painter that transforms its
frame before painting in it.
For example, if p is a painter and f is a frame, then
(p ((make-relative-frame (make-vect .5 .5) (make-vect 1 .5) (make-vect .5 1)) f))
will paint in the upper-right-hand corner of the frame.
We can abstract this idea with the following procedure:
(define (make-painter-transformer origin corner1 corner2) (lambda (painter) (compose painter (make-relative-frame origin corner1 corner2))))
This procedure is of type
. Note how the
type helps us understand the ways in which
make-painter-transformer can be used, i.e., its returned value must
take a painter as input and will return a painter, which means by
closure that the result can be again subjected to any other transformer.
Calling make-painter-transformer with an origin and two corners
returns a procedure that transforms a painter into one that paints
relative to a new frame with the specified origin and corners. Note
how it accomplishes this - it uses make-relative-frame to
return a procedure that takes a frame as argument and returns a new
frame. Thus when the procedure returned by make-painter-transformer is
applied to a painter, the expression involving compose first
applies this new frame procedure to the initial frame, and creates a new
frame to which the painter is then applied.
For
example, we could define:
(define (shrink-to-upper-right painter) ((make-painter-transformer (make-vect .5 .5) (make-vect 1 .5) (make-vect .5 1)) painter))
Another way to define shrink-to-upper-right is:
(define shrink-to-upper-right (make-painter-transformer (make-vect .5 .5) (make-vect 1 .5) (make-vect .5 1)))
Another transformed frame, called flip-horiz should flip images
horizontally (we'll ask you to implement this later), another
rotates images counterclockwise by 90 degrees:
(define rotate90 (make-painter-transformer (make-vect 1 0) (make-vect 1 1) (make-vect 0 0)))
and similar rotations, rotate180 and rotate270, can be created.
We can combine the results of two painters in a single frame by calling each painter on the frame:
(define (superpose painter1 painter2) (lambda (frame) (begin (painter1 frame) (painter2 frame))))
Superpose is of type 
.
To draw one image beside another, we combine one in the left half of the frame with one in the right half of the frame:
(define (beside painter1 painter2) (let ((split-point (make-vect 0.5 0.0))) (superpose ((make-painter-transformer (make-vect 0.0 0.0) split-point (make-vect 0.0 1.0)) painter1) ((make-painter-transformer split-point (make-vect 1.0 0.0) (make-vect 0.5 1.0)) painter2))))
We can also define painters that combine painters vertically, by using rotate together with beside. The painter produced by below shows the image for painter1 below the image for painter2:
(define (below painter1 painter2) (rotate270 (beside (rotate90 painter2) (rotate90 painter1))))
You should prepare the following exercises for oral presentation in tutorial. They cover material in sections 2.1 and 2.2 of the text, and they also test your understanding of the square-limit language described above, in preparation for doing this week's lab exercises. You may wish to use the computer to check your answers to these questions, but you should try to do them (at least initially) without the computer.
Draw box-and-pointer diagrams for the lists a and b defined as follows:
(define a (list 2 3 5)) (define b (append a (reverse a)))
where append and reverse are built-in procedures that could be defined as follows:
(define (append x y) (if (null? x) y (cons (car x) (append (cdr x) y))))
(define (reverse x) (define (iter x y) (if (null? x) y (iter (cdr x) (cons (car x) y)))) (iter x '()))
Demonstrate that make-painter-transformer is of the type stated above. What does
(compose (make-painter-transformer (make-vect 0 0) (make-vect 0.5 0) (make-vect 0 1)) (make-painter-transformer (make-vect 0.5 0) (make-vect 1 0) (make-vect 0 1)))
do? Use types to verify your answer, and if needed use the substitution model to work things through.
If you are going to try to do the problem set at home or on Athena, then be sure to read the Problem Set 4 Warning File on the 6.001 web site for special directions. Also be sure to leave yourself enough time so that you can still go to the lab and get your work done, if the Athena or PC version does not work.
Load the code for problem set 4, which contains the procedures described in section 1. You will not need to modify any of these. We suggest that you define your new procedures in a separate (initially empty) editor buffer, to make it easy to reload the system if things get fouled up.
When the problem set code is loaded, it will create three graphics windows, named g1, g2, and g3. To paint a picture in a window, use the procedure paint. Paint takes a graphics window and a painter, determines the frame for the graphics window, and gives the frame to the painter. For example - once you have successfully completed lab exercise 1 and successfully evaluated (load-rest) - then
(paint g1 fovnder)
will show a picture of William Barton Rogers in window g1.
There is also a procedure called paint-hi-res, which paints the
images at higher resolution ( 
rather than 
). Painting at a higher resolution produces better looking
images, but takes four times as long. As you work on this problem
set, you should look at the images using paint, and reserve
paint-hi-res to see the details of images that you find
interesting.
If you work on the problem set in multiple sessions, be sure that you reload this file after you have loaded up the problem set, so that your new definitions will override the ones in the problem set file. You will also have to redo the (load-rest) evaluation described below.
Turn in a listing of your code, and some examples of using it.
Once you have created your data abstractions, evaluate
(load-rest)
to have the rest of the code for the problem set loaded into your Scheme environment.
Make a collection of primitive painters to use in the rest of this lab. In addition to the ones predefined for you (and listed in section 1), define at least one new painter of each of the four primitive types: a uniform grey level made with number->painter, something defined with procedure->painter, a line-drawing made with segments->painter, and an image of your choice that is loaded from the 6001 image collection with image->painter. Turn in a list of your definitions.
Earlier we referred to examples of transforming painters, i.e. procedures that take a painter as input and create a new painter that will draw relative to some new frame. Increase the repetoire of such methods by implementing a transformation, flip-horiz, which takes as input a painter, and returns a new painter that draws its input flipped about the horizontal axis. Also implement rotate180 and rotate270 in analogy to rotate90. Turn in a listing of your procedures.
Experiment with some combinations of your primitive painters, using beside, below, superpose, flips, and rotations, to get a feel for how these means of combination work. You needn't turn in anything for this exercise.
The ``diamond'' of a frame is defined to be the smaller frame created by joining the midpoints of the original frame's sides, as shown in figure 4. Define a procedure diamond that transforms a painter into one that paints its image in the diamond of the specified frame, as shown in figure 4. Try some examples, and turn in a listing of your procedure.
Figure unable to convert from postscript
The ``diamond'' of a frame is formed by joining the midpoints
of the sides. This is illustrated with a painting created by (diamond fovnder).
The ``diamond'' transformation has the property that, if you start with a square frame, the diamond frame is still square (although rotated). Define a transformation similar to diamond, but which does not produce square frames. Try your transformation on some images to get some nice effects. Turn in a listing of your procedure.
The following recursive right-split procedure was demonstrated in lecture:
(define (right-split painter n) (if (= n 0) painter (let ((smaller (right-split painter (- n 1)))) (beside painter (below smaller smaller)))))
Try this with some of the painters you've previously defined, both primitives and combined ones. Now define an analogous up-split procedure as shown in figure 5. Make sure to test it on a variety of painters. Turn in a listing of your procedure. (In defining your procedure, remember that (below painter1 painter2) produces painter1 below painter2.)
Figure 5:
The up-split procedure places a picture below two (recursively)
up-split copies of itself. This was created from (up-split fovnder 4)
Right-split and up-split are both examples of a common pattern that begins with a means of combining two painters and applies this over and over in a recursive pattern. We can capture this idea in a procedure called keep-combining, which takes as argument a combiner (which combines two painters). For instance, we should be able to give an alternative definition of right-split as
(define new-right-split (keep-combining (lambda (p1 p2) (beside p1 (below p2 p2)))))
Complete the following definition of keep-combining:
(define (keep-combining combine-2) ;; combine-2 = (lambda (painter1 painter2) ...) (lambda (painter n) ((repeated
fill in missing expression
n) painter)))
where repeated is given by:
(define (repeated f n) (if (zero? n) identity (compose f (repeated f (- n 1)))))
Show that you can indeed define right-split using your procedure, and give an analogous definition of up-split.
Once you have keep-combining, you can use it to define lots of recursive means of combination. Figure 6 shows an example, which comes from:
(define nest-diamonds (keep-combining (lambda (p1 p2) (superpose p1 (diamond p2)))))
(nest-diamonds fovnder 4)
Invent some variations of your own. Turn in the code and one or two sample pictures.
Figure unable to convert
Some recursive combination schemes, defined with keep-combining.
The procedures you have implemented give you a wide choice of things to experiment with. Invent some new means of combination, both simple ones like beside and complex higher-order ones like keep-combining and see what kinds of interesting images you can create. Turn in the code and one or two figures.
Hopefully, you generated some interesting designs in doing this assignment. If you wish, you can enter printouts of your best designs in the 6.001 PS4 design contest. Turn in your design collection together with your homework, but stapled separately, and make sure your name is on the work. For each design, show the expression you used to generate it. Designs will be judged by the 6.001 staff and other internationally famous art critics, and fabulous prizes will be awarded in lecture. There is a limit of two entries per student. Make sure to turn in not only the pictures, but also the procedure(s) that generated them.
How much time did you spend on this problem set?
If you cooperated with other students working this problem set please indicate their names on your solutions. As you should know, as long as the guidelines described in the 6.001 Policy on Cooperation handout are followed, such cooperation is allowed and encouraged.
This document was generated using the LaTeX2HTML translator Version 96.1-f (May 31, 1996) Copyright © 1993, 1994, 1995, 1996, Nikos Drakos, Computer Based Learning Unit, University of Leeds.
The command line arguments were:
latex2html -split 0 ps4hend.tex.
The translation was initiated by Jeremy Daniel on Tue Feb 25 04:50:03 EST 1997