 |
Problem Set 2
Your goals for this problem set are three-fold. First, you will gain practice with Scheme mechanisms for compound data (specifically, pairs created using cons). Second, you will become expert in manipulating both lists and trees, which are important conventional interfaces we often use to represent more complicated or hierarchical data. Finally, an important aspect of Scheme programming is learning to write and use higher order procedures; the third goal of this problem set is for you to become skilled in writing higher order procedures and analyzing the processes they generate.
While this problem set has a large number of computer exercises, you are primarily being asked to write many small procedures to gain practice, rather than understand or write a large software system. Your software development will go much faster if you can take advantage of previous procedures when you write new ones.
You should prepare these exercises for oral presentation in tutorial and include written answers in your homework solution.
Each of the following expressions are evaluated, in the order they appear. At the indicated point, show what the returned value would be, and draw a box and pointer diagram corresponding to the returned value (if the returned value is a pair). You will need to understand the printed representation of pairs and lists, as well as how the above primitive procedures work.
(define x (cons 1 2)) (define y (cons x x)) y ==> ?? (define a (cons 1 (cons x (cons 3 nil)))) a ==> ?? (define b (list 1 x 3)) b ==> ?? (null? (cdddr b)) ==> ??
(last-pair (list 23 72 149 34)) ==> (34)
Define a closely related procedure last that returns the last element of a given (nonempty) list:
(last (list 23 72 149 34)) ==> 34
Next define copy using map, then using filter, and finally using accumulate. As you do this, note the similarity in structure between your directly implemented copy and each higher order procedure.
(define (map p sequence) (accumulate (lambda (x y) <??>) nil sequence)) (define (append seq1 seq2) (accumulate cons <??> <??>)) (define (length sequence) (accumulate <??> 0 sequence))
(list 1 (list 2 3) (list 4 (list 5)))
Give the result printed by the interpreter, show the corresponding box and pointer diagram, and draw the interpretation of this structure as a tree (as in Figure 2.6 in SICP on page 108).
Do exercise 2.28 of the text, to implement a procedure fringe which operates on a tree that is represented using nested lists, and produces a flattened list of the leaves (in left to right order) in the tree.
One important application of computer science is in the financial markets. Communication and information technology is crucial to the management of vast amounts of market information, and sophisticated signal processing and artificial intelligence technology is often applied in an effort to, well, make money, by careful observation of the stock market.
In this section, we will track a fictional company, Acme Industries, as it is traded on the floor of the New York Stock Exchange (NYSE). We will find that list manipulation procedures can be used to help calculate information about the price and trading activity in the stock. Note that we will be manipulating lists - the government frowns upon manipulation of the stock market itself.
First, let us consider a simplified version of a stock ticker, or a list of stock prices. Our price ticker will be a sequence (list) of the stock prices that our stock, Acme in this case, has traded at throughout any given trading day. On the NYSE, stock prices are given in dollars and fractions of dollars (down to 1/16th of a ``point''); we will use real numbers to indicate prices. For example, on the previous day IBM closed at 101.0, and for the current trading day, the price ticker for IBM might look like:
(define ibm-previous-close 101.0) (define ibm-prices (list 100.0 99.5 99.5 99.75 100.0 100.125 100.5))
In this part, you will write basic procedures to perform simple technical analysis on these prices.
Begin by loading the code for problem set 2, using the Edwin command M-x load problem set. This will define for you the variable acme-prices to represent our ticker, as well as give you the basic list procedures map, filter, and accumulate.
Write a procedure price-trend that calculates the net gain (a positive number) or loss (a negative number) in the price of the stock based on the closing price (last price) of the current trading day compared to the closing price on the previous day. The procedure should take as arguments the previous day's closing price and the day's ticker for the stock, e.g. (price-trend <previous-close> <ticker>). You should feel free to use the basic list higher order procedures above, or any procedures you defined in the tutorial exercises.
(price-trend ibm-previous-close ibm-prices) ==> -0.5
Demonstrate that price-trend works on some simplified cases of your own, and then show the price-trend result for Acme Industries. Note that variables acme-previous-close and acme-prices are defined in the problem set code for you.
Is the process your procedure generates iterative or recursive? What is the order of growth in space S and computation time T as a function of the length N of the ticker? (For this case, you should look for the depth of deferred operations to indicate space, and examine the number of basic cons, car, and cdr operations when considering time.)
Is the process your procedure generates iterative or recursive? What is the order of growth in terms of space S and computation time Tas a function of the length of the ticker?
Write a procedure price-high that returns the highest price of the stock during the trading day. This is just a call to a new higher order procedure you are to write named list-max that returns the largest item in the list:
(define (price-high ticker) (list-max ticker)) (price-high ibm-prices) ==> 101.5
You should write the list-max procedure so that it walks over the data structure directly (i.e. does not use the higher order procedures map, filter, or accumulate, but rather uses car, cdr, null?). You may also find the Scheme procedure max, e.g. (max 27 35) ==> 35 helpful.
Does your procedure produce an iterative or recursive process? Now write it the other way (i.e. if you first wrote a recursive process version, write an iterative version, or vice-versa). As always, in both cases show simple test cases, and show the high price of the day for Acme Industries.
Now you may take advantage of the existing conventional list interfaces and higher order procedures. Rewrite your price-high procedure using accumulate.
The use of the accumulate procedure (as defined in the book and in the problem set code) by price-high results in a recursive process - explain why.
Our ace stock analyst Ben Bitdiddle wants to create a general iterative version of accumulate. Consider the following attempt:
(define (iter-accumulate combiner init lst)
(define (helper so-far lst)
(if (null? lst)
so-far
(helper (combiner (car lst) so-far)
(cdr lst))))
(helper init lst))
Can Ben correctly rewrite price-high to use iter-accumulate with a reduced order of growth in space or time?
Ben proposes to the head of the firm, Alyssa P. Hacker, that all procedures that currently use accumulate should be converted to use iter-accumulate. Alyssa disagrees, and states that it would be wrong to use iter-accumulate interchangeable with accumulate. Help show what Alyssa means by (1) giving a counter-example where different results would be obtained with accumulate and iter-accumulate; and (2) explaining under what conditions it would be safe to use iter-accumulate in place of accumulate.
(define (price-range ticker)
(list (price-low ticker)
(price-high ticker)))
Unlike the procedure above, however, Ben is asked to write the procedure in such a fashion that it only walks over the ticker once (whereas the procedure above must walk over the list twice). Complete Ben's procedure below, and show the price-range for Acme's stock:
(define (price-range ticker)
(define (helper ticker low-so-far high-so-far)
(if (null? ticker)
<??>
(helper <??>
(min <??> <??>)
(max <??> <??>))))
(helper (cdr ticker) (car ticker) (car ticker)))
So far we have just considered the ticker tape of prices. Now let's go onto the ``floor'' and consider in more detail the way in which trades (buying and selling) of stock occur.
In stock trading, the ask or offer-price is what a seller offers to sell at, while the bid-price is what a buyer is willing to pay. In both cases, the offerer or bidder must say not only what price she or he desires, but also the number of shares that the offer or bid applies to. We will use a Scheme pair (cons cell) to represent a bid as the combination of the bid-price and number of shares (or bid-shares), and will similarly represent the offer as the combination of the ask-price and ask-shares. (Note that we will use the term offer or ask interchangeably.)
(define (ask-price ask) (car ask)) (define (ask-shares ask) (cdr ask)) (define (bid-price bid) (car bid)) (define (bid-shares bid) (cdr ask))
In this exercise, we assume an idealized market in which an offer is made, followed immediately by a bid, followed by another offer, and so on in a paired alternating fashion. Suppose we now have a record of the bid and ask prices for our stock (by our rules above these two lists will always be of equal length):
(define ibm-ask (list (cons 101.0 200) (cons 100.5 200) (cons 101.0 100))) (define ibm-bid (list (cons 100.5 100) (cons 100.5 100) (cons 101.0 100)))
The spread is the difference between the ask price and the bid price. When the spread becomes zero (or less than zero, although the rules are such that this should not occur), a trade will occur at the agreed upon price. For example, in the second round of the above case someone offers 200 shares of IBM for 100 1/2, and someone agrees to buy just 100 of those shares for 100 1/2. The difference or spread in price has gone to zero, and 100 shares change hands.
To begin, write this so that your procedure directly walks over the two lists (e.g. using car, cdr, cons, null?, and appropriate accessor functions). Is your process recursive or iterative, and what are the orders of growth in space and time? Show the list of spreads for Acme stock over the day.
(map2 + (list 1 2 3) (list 10 11 12)) ==> (11 13 15)
Re-implement your price-spreads procedure to use map2.
Now given a list of offers and a list of bids as above, we wish to produce as output the ticker of stock prices (consisting only of the prices at which shares have actually exchanged hands) such as we saw in computer exercise 1. Write a procedure ticker-prices that works as:
(ticker-prices ibm-asks ibm-bids) ==> (100.5 101.0)
(merge2 (lambda (x y) (and (odd? x) (odd? y)))
+
(list 1 2 3 4)
(list 5 3 5 3))
==> (6 8)
Complete the code for this merge2 higher order procedure:
(define (merge2 pred proc list1 list2)
(cond ((null? list1) nil)
((<??> (car list1) (car list2))
(cons (<??> (car list1) (car list2))
(<??> pred proc (cdr list1) (cdr list2))))
(else (<??> pred proc (cdr list1) (cdr list2)))))
(define (ticker-prices asks bids)
(merge2 trade?
(lambda (ask bid) (car ask))
asks bids))
In the daily stock market report, the public is often very interested in knowing the volume (total number of shares traded). Using the merge2 procedure, write a new procedure (ticker-shares <ask-list> <bid-list>) that produces a list consisting of the number of shares for each individual trade (again, just for those cases where a trade actually occurs). Show how this can be used with accumulate to create a procedure total-shares that takes the asks and bids, and produces the the total number of shares exchanged. Show the ticker-shares and total-shares results for Acme.
We now have the opportunity to visit Acme's manufacturing plant to understand better how they assemble their products. Acme makes widgets. A widget is a complex object assembled from some number of smaller components. Each of these components may also be made up of smaller subcomponents, and this ``nesting'' of subcomponents can be arbitrary deep for arbitrarily complex widgets. Acme needs representations to help (a) manage the time and number of manufacturing stations needed to build widgets, (b) manage the number of components that go into a widget, and (c) analyze the cost of building widgets.
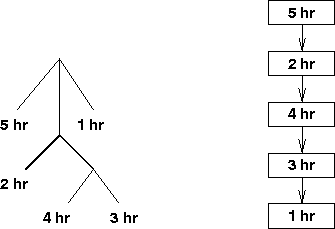
The first challenge is to represent the sequence of operations and time required to build widgets. Acme uses a tree structure as illustrated in Figure 1 to indicate both the overall structure of their assembly procedure, and the time required to put together parts. A leaf is inserted into the tree for each ``manufacturing station,'' which is the physical location on the plant floor where people and machines assemble some particular subcomponent. For this leaf in the tree, Acme indicates the number of hours it takes to assemble that component or part of the widget. If a part that is going into the assembly must itself be assembled, then that part is represented as a subtree (or ``node'') rather than as the number of hours. For example, the brand new ``NeoWidget'' that Acme has recently begun selling consists of three top-level operations (as illustrated in Figure 1): putting the backplane together (taking 5 hours), putting the various sprockets together and into the backplane (which can take up to 9 hours), and putting the operator controls on the front (which takes 1 hour). The assembly of the sprockets is an assembly suboperation, which consists of assembling a frob (2 hours), together with a doo-dad consisting of some big sprockets (4 hours) and some small sprockets (3 hours). The assembly hours representation is:
(define NeoWidget-hours (list 5 (list 2 (list 4 3)) 1))
which is drawn in a tree form as shown in Figure 1. For now, we will assume that manufacturing occurs in a sequential assembly line fashion, where the product moves from one manufacturing station to the next in sequence. In the case of the NeoWidget, the assembly line consists of a sequence of five stations.
 |
In the problem set code, the assembly tree for the Acme ``MegaWidget'' is also defined (provided as MegaWidget-hours). Show the number of hours required to make a MegaWidget using an assembly line.
(define (tree-accumulate combiner op initial tree)
(cond ((null? tree) <??>)
((not (pair? tree))
(<??> tree))
(else
(<??> (tree-accumulate combiner op initial (<??> tree))
(tree-accumulate combiner op initial (<??> tree))))))
Now rewrite your assembly-line-hours to use this procedure.
As the whiz-bang outside consultant, you have been asked to see if there is any way to speed up the assembly process and shorten the manufacturing time for the product. You argue that many of the operations can be performed in parallel rather than in sequence. In discussion with the manufacturing personnel, they determine that parts can indeed be assembled in parallel; however each subassembly (indicated by a node rather than a leaf in the tree assembly representation) will then require an additional assembly work station to put together the sub-assemblies coming from the respective parallel stations. In the previous assembly line situation, nodes did not require a work station, as assembly only took place (in left to right sequence) at points corresponding to leaves in the tree. One additional hour will also be needed at each of these ``merge'' stations. This situation is shown schematically in Figure 2. Thus, for the NeoWidget, an additional hour (and work station) is needed after the completion of the 3 hour and 4 hour parallel operations; another hour (and station) is need to then merge with the parallel 2 hour operation, and a final additional hour (and a third additional station) is needed to merge with the parallel 5 and 1 hour operations; thus a total of 7 hours (and 8 work stations) will be required. Note that we are ``pipelining'' multiple instances of the same part number through the assembly line or parallel assembly flow, so that when one part (serial number) moves to the next station, the next part (with the next serial number) comes into that station. For this reason, we do not ``share'' or reuse stations that might appear to be unoccupied because of the sequencing requirements.
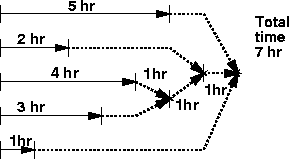 |
Hint: this will be one hour more than the maximum number of hours it takes to parallel assemble all the subcomponents of the widget. You may also find higher order procedures defined earlier, such as list-max, to be helpful, together with wishful thinking.
How long will it take to assemble a MegaWidget in parallel?
How many manufucturing stations are needed if we parallel produce the MegaWidget?
Acme is interested to know how much more quickly the NeoWidget (and in general any product) can be built if the underlying operation time could be reduced by some factor. For example, suppose the pure assembly time (corresponding to leaves in the original assembly tree) could be halved for all sub-assemblies, but the ``merge'' time of one hour remains for each of the additionally required merge stations. Clearly, the overall manufacture time is not in general half that of the original, because of the overhead of the merge time. For example
(parallel-scale 0.5 NeoWidget) ==> 0.643 ; from 4.5/7.0
Write the procedure parallel-scale that takes as the first argument the factor by which we are able to scale the primitive assembly operations, takes as the second argument the assembly tree for some product, and returns the fraction of time the new manufacturing plant would take assuming parallel assembly. You may find it useful to implement a procedure map-tree which maps some procedure over the leaves of a tree to produce a new tree; this can be easily be implemented in terms of accumulate-tree.
What is this time benefit if we cut the raw assembly time for the MegaWidget in half?
In addition to the assembly time, Acme is interested in determining the component or part counts and costs for its widgets. Again, a tree representation is chosen. The parts-count tree mirrors the structure of the previous assembly tree, with one important difference: for each leaf node in the assembly tree (where we indicated the number of hours required to assemble that component), the parts-count tree instead has a list of the numbers of different kinds of purchased parts that are needed for assembly of that component.
In addition, the parts-cost tree is structured in parallel to the parts-count tree, but giving the cost (in dollars) of each of the corresponding primitive parts used in that assembly. These two new tree data structures are illustrated for the NeoWidget in Figure 3.
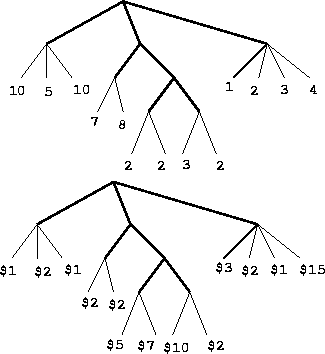 |
A possible strategy is to walk all three trees together, but use the structure of the assembly tree to guide what to do with the other two trees. Create a summarized costs tree for the MegaWidget.
This document was generated using the LaTeX2HTML translator Version 98.1p1 release (March 2nd, 1998)
Copyright © 1993, 1994, 1995, 1996, 1997, Nikos Drakos, Computer Based Learning Unit, University of Leeds.
The command line arguments were:
latex2html ps2-listprocs.
The translation was initiated by Duane Boning on 1998-09-14