Matrices are not the only (or best) way of representing rotations. For one thing, they are redundant (9 numbers instead of 3) and, for another, they are difficult to interpolate.
An alternative representation was developed by Hamilton in the early 19th century (and forgotten until relatively recently). The quaternion is a 4-tuple of reals with the operations of addition and multiplication defined. Just as complex numbers allow us to multiply and divide two-dimensional vectors, quaternions enable us to multiply and divide four dimensional vectors.


A quaternion can also be interpreted as having a scalar part and a vector part. This will give us a more convenient notation.


Quaternion addition is just the usual vector addition, the quaternion product is defined as:
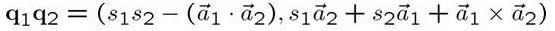