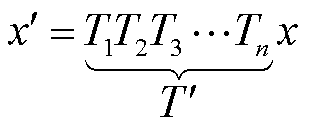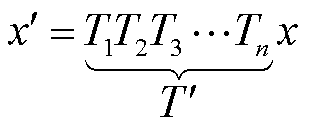For Translations:

1. There exists an inverse mapping for each function
2. There exists an identity mapping
3. The composition operation is associative
4. The functions are "closed under composition"

These properties might seem trivial at first glance, but they are actually very important, because when these conditions are shown for any class of functions and their two-argument composition operation, then they form an algebraic group. One of the consequences is that any series of translations can be composed to a single translation. Another consequence is that the inverse is unique.
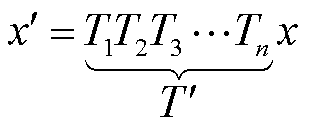