This transformed tangent, t', must be perpendicular to the transformed normal, n'. Let's solve for the transformation, Q that maintains this relationship.

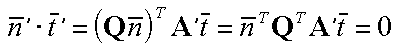
All that we need to do is find a value for the Q matrix so that the transformed normal and the transformed tangent are still orthogonal. This can be accomplished by letting

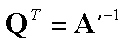
which gives

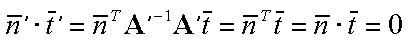
Thus the transform that must be applied to normals so that they remain perpendicular to the tangent space of transformed points is:

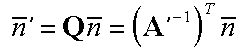Is there a class of matrices where (A'^-1)^T = A?