 |
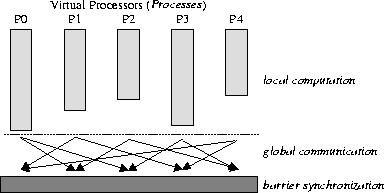
In BSP, a parallel program runs across a set of virtual processors (called processes to distinguish them from physical processors), and executes as a sequence of parallel supersteps separated by barrier synchronizations. Each superstep is composed of three ordered phases, as shown in Fig. 1: 1) a local computation phase, where each process can perform computation using local data values and issue communication requests such as remote memory reads and writes; 2) a global communication phase, where data is exchanged between processes according to the requests made during the local computation phase; and 3) a barrier synchronization, which waits for all data transfers to complete and makes the transferred data available to the processes for use in the next superstep.
Figure 2 shows pseudo-code for a simple program where each process passes data to its right neighbor and performs a little local computation. As shown, BSP is very similar to conventional SPMD/MPMD (single/multiple program, multiple data)-based programming models such as MPI, and is at least as flexible, having both remote memory (e.g., bsp_put()) and message-passing (e.g., bsp_send() and bsp_recv()) capabilities. The timing of communication operations, however, is different - since the global communication phase does not happen until all processes finish the local computation phase, the effects of BSP communication operations are not felt until the next superstep. In line 6 of Fig. 2, for example, s gets the unchanged local value of d. Similarly, in line 9, the call to bsp_recv() returns null or generates an exception.
This postponing of communications to the end of a superstep is the key idea in BSP. It removes the need to support non-barrier synchronizations between processes, and guarantee that processes within a superstep are mutually independent. This makes BSP easier to implement on different architectures than traditional models, and makes BSP programs easier to write and to analyze mathematically. For example, since the timing of BSP communications make circular data dependencies between BSP processes impossible, there is no risk of deadlock or livelock in a BSP program. Also, the separation of the computation, communication, and synchronization phases allows one to compute time bounds and predict performance using relatively simple mathematical equations [20].
Because of these advantages, a growing number of people are now applying BSP to a wide variety of realistic parallel applications [5], ranging from small general-purpose numeric libraries (e.g., for matrix operations), to large computational research applications used in both academia and industry (e.g., computational fluid dynamics, plasma simulation, etc.). By implementing BSP in Java, we hope to enable programmers to port these applications to Java, and make it easier to do realistic research using volunteer computing systems.