next up previous




MASSACHVSETTS INSTITVTE OF TECHNOLOGY
Department of Electrical Engineering and Computer Science
6.001--Structure and Interpretation of Computer Programs
Fall Semester, 1998


Problem Set 1

Henceforth, problem sets will consist of two parts:

You must hand in written solutions to both the tutorial exercises and the programming assignments. Solutions should be handed in at the beginning of recitation, and late work will not be accepted. Your tutor will look over the homework you hand in and review it with you in tutorial.

The purpose of this problem set is to familiarize you with procedural abstractions by having you write Scheme code within a cryptographic context. We recommend that you first skim through the problem set in its entirety to familiarize yourself with the format.

In addition, there is a section entitled ``Debugging Tools'' which is a computer exercise designed to acquaint you with Scheme's debugging facilities. There is nothing to turn in for the ``Debugging Tools'' section, but we highly recommend that you take the time to go through the exercise, since knowledge of the debugging tools can save you a lot of time on future problem sets.

Cryptography: Message Security1

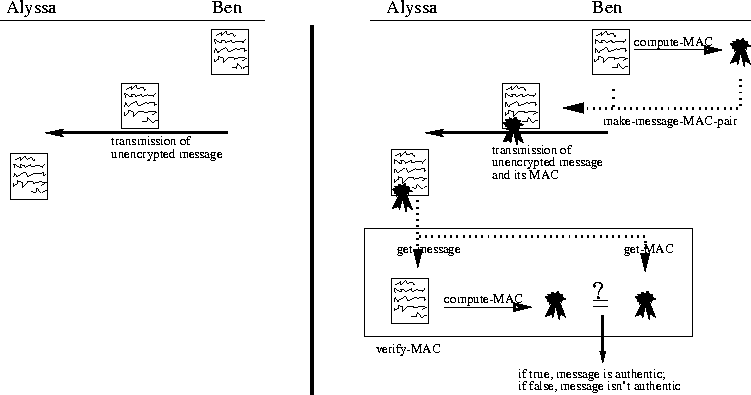
Alyssa P Hacker receives a message from her colleague, Ben Bitdiddle.2 It says "Ok to let Dan Glen F Frince borrow the laptop at 9pm tonight". Note that the contents of this message is sent in the clear, so it is unencrypted and readable by anyone who happens to intercept the message (see Figure 1, left portion). If this is the case, how does Alyssa know that the message was actually sent from Ben and that it was not tampered with and modified somehow while in transit? The need to authenticate the originator of a message is crucial for many applications such as authorized payments, purchase orders, stock quotes and official press releases. However, there is often a need to keep the contents of a message private. This is known as message confidentiality, and when combined with message authentication is useful for grade reports, military commands, medical records, bank statements, and many other applications.

In this problem set, we'll first look at message authentication and then consider message confidentiality.

1. Message Authentication

When Alyssa considers a message from Ben to be authentic, she believes two things:

There are two methods for authenticating messages: MACs (Message Authentication Codes) and digital signatures. We will consider the former here.

A MAC is a key-dependent one-way hash function. In English, that means that the MAC is a function that takes as inputs the message (however long) and a ``key'' (usually a large number) and outputs a (usually fixed-length) value called the ``hash''. A hash function is ``one-way'' if it is difficult to generate a message that hashes to a specific desired hash value even if the key and hash function is publicly known. Thus, it is easy to compute the MAC for a given message, but it is nontrivial to find another message, distinct from the first, that will hash to the same value because the function is non-invertible.

Let's assume Alyssa and Ben somehow agree on a shared key K (i.e. they both know the value of K). We can assume for now that they either arrange to meet privately or they choose K while talking on the phone. When Ben sends his message to Alyssa (see Figure  1, right portion), he can append to his message, a MAC computed using his message and K. This MAC is represented in the figure as a seal affixed to the message. When Alyssa receives this transmission, she is able to separate the message from the MAC, and since she and Ben alone know the value of K, she can also compute the MAC to verify it against the MAC appended to the message.


  
Figure 1: Communication between Alyssa and Ben, without authentication (left) and with authentication (right)
\begin{figure} \mbox{\epsfbox{authentication.eps}} \epsfysize=2in \end{figure}

If the MACs match, Alyssa has now authenticated the message. Since only Alyssa and Ben know K, only Ben could have computed this MAC successfully. Furthermore, since it is hard to find another message (distinct from Ben's original message) that produces the same MAC, Alyssa can rest assured that she received the original message intact. Note the distinction between encryption and authentication - the MAC is not an encryption of the message; indeed the message used to compute the MAC must be sent in the clear (unencrypted) in order for the MAC to be verifiable.

Implementing Message Authentication

For computing the MAC, we will use MD53, a one-way hash function invented by Ron Rivest.4 We've provided a procedure called compute-MAC which takes a text string message and a numeric key, appends the key (converted to a string representation) to the message, and uses this concatenated result as the input to the MD5 algorithm which produces a 128-bit value.

For example, 

(compute-MAC "My little message" 87193)
;Value: 221894140609816864960426026903967285567

Message-MAC Pairs

Once Ben has written his message m and computed its MAC, he prepares the following message, message-from-Ben, which is transmitted to Alyssa: 

(define message-from-Ben (make-message-MAC-pair m MAC))

The procedure make-message-MAC-pair is an example of a data constructor. All it does is packages a message and its MAC together. Once a message-MAC-pair has been constructed, we can select each of the individual pieces by using data selectors: get-message and get-MAC. Each of these take the message-MAC-pair as an argument. Constructors and selectors are all very simple procedures, and they are discussed in lecture on September 17.

Authenticating a Received Message

When Alyssa receives a message from Ben, she needs to be able to verify the authenticity of the message. We will leave it to you to implement the procedure verify-MAC which takes as input a message-MAC-pair and a shared key, and outputs true if the MAC computation checks out, and false if it doesn't.

Alternate MAC Implementations

In the above scenario, we simply concatenated the key to the beginning of the message and used the result as input to the MAC computing algorithm. In many cases, this may not be secure, and may be subject to cryptanalysis. In other words, if someone has obtained a number of different messages and their corresponding MACs, all computed using the same key, it maybe be possible to figure out what the shared secret key is.

Often, people experiment with different ways to combine the message and the key. One possibility might be to apply the MAC repeatedly: compute the MAC as before, concatenate the key to this and use the result as input to the MAC algorithm again. This process could be repeated a number of times.5 You will work on and write procedures: recursive-compute-MAC and iterative-compute-MAC which do just this.

Arriving at a Shared Secret: Diffie-Hellman Key Exchange

In the above scenario, both Alyssa and Ben needed to possess the shared secret key K. But always arranging to meet in person to agree on a key can be inconvenient, and talking on the phone or sending email can be insecure.

Fortunately, the Diffie-Hellman Key Exchange is a method by which two people can compute a shared secret that will be known only to the two of them, even though all the communication that transpires between them is public! (see Figure  2)


  
Figure 2: Alyssa and Ben agreeing on a secret key K
\begin{figure} \mbox{\epsfbox{exchange.eps}} \epsfysize=1.5in \end{figure}

If Alyssa and Ben wish to communicate, first they agree (in public) on a large prime number p and a number g which is a generator for p. (For g to be a generator means that the powers $g,g^2,g^3,\ldots, g^{p-1}$, taken modulo p, produce all the integers $1,2,3,\ldots, p-1$, in some order.)

Alyssa picks a secret number a and computes $k_a \equiv g^a \bmod p$.6 Ben picks a secret number b and computes $k_b \equiv g^{b} \bmod p$. Alyssa sends Ben ka, and Ben sends Alyssa kb (alternatively, they both simply publish these numbers; in either case, they can be assumed to be publicly known values). Having obtained kb, Alyssa now computes $(k_b)^a \bmod p$ and similarly, Ben, having received ka, computes $(k_a)^{b} \bmod p$. But these are the same number because


\begin{displaymath}k_b^a \equiv (g^{b})^a \equiv g^{ba} \equiv g^{ab} \equiv (g^a)^{b} \equiv k_a^{b} \bmod p \equiv K \end{displaymath}

Now that Alyssa and Ben have this shared number (which we have been calling K), they can now use K as a key for sending and receiving MAC-authenticated messages.

Note that during this protocol, all communication between Alyssa and Ben was public. An eavesdropper possessing the values ka and kb (and also p and g) would still not be able to find K. If p is a large prime, there is no efficient way to compute K.

Implementing Diffie-Hellman Key Exchange

Our main tools for implementing encryption and decryption are computing primes and doing fast modular exponentiation as in section 1.2.6 of the textbook.

We have the procedure that computes a power of a number modulo another number: 

(define (expmod b e m)
  (cond ((zero? e) 1)
        ((even? e)
         (modulo (square (expmod b (/ e 2) m)) m))
        (else
         (modulo (* b (expmod b (-1+ e) m)) m))))

We also have the Fermat test which we will use to test for primality:7 

(define (fermat-test n)
    (let ((a (choose-random n)))
      (= (expmod a n n) a)))

To test if a number n is prime, we use fast-prime? to run the fermat-test on n some specified number of times. 

(define (fast-prime? n times)
    (cond ((= times 0) true)
          ((fermat-test n) (fast-prime? n (- times 1)))
          (else false)))

To generate a prime, we pick a random value with a specified number of digits and start testing successive odd numbers from there until we find a prime. We'll consider a number to be prime if it passes two rounds of the Fermat test. 

(define (choose-prime digits)
  (let ((range (expt 10 (- digits 1))))
    ;;start with some number between range and 10*range
    (let ((start (+ range (choose-random (* 9 range))))) 
    (search-for-prime (if (even? start) (+ start 1) start)))))

(define (search-for-prime guess)
  (if (fast-prime? guess 2)
      guess
      (search-for-prime (+ guess 2))))

Finding generators: safe primes

Unfortunately, it's not enough just to find a prime. We also have to find a generator for the prime modulus. Finding a generator for an arbitrary prime can be complicated, but there is a certain kind of prime, safe primes, for which it is easy. A safe prime is a prime number p of the form 2q+1 where q is also prime. The following theorem lets us compute generators for safe primes:8

If p=2q+1 is a safe prime, then for any number $2 \leq g \leq p-2$ either $g^2 \equiv 1 \bmod p$, or $g^q \equiv 1 \bmod p$, or g is a generator for p.

We can use these ideas as follows:

Your job is to write a procedure to generate safe primes and another to find a generator.

Key Systems

There are four numbers involved in the Diffie Hellman key exchange: p, g, a secret x (a for Alyssa, b for Ben) and a function of this secret, $y=g^x \bmod p$ (ka for Alyssa and kb for Ben). Let's refer to these four numbers collectively as a key system. The part kept secret by each party is the value of x. The public part of this, namely, p, g, and y, we'll call a published key. Alyssa(Ben) needs Ben's(Alyssa's) published key to compute the shared key K. 

(define (generate-key-system-parameters digits)
  (let ((p (choose-safe-prime digits)))
    (let ((g (find-generator p)))
       (create-key-system p g))))

(define (create-key-system p g)
  (let ((x (choose-random p)))      ;x will be secret
    (let ((y (expmod g x p)))       ;y will be public
       (make-key-system p g x y))))

Note that it is necessary that Alyssa and Ben use the same p and g. For example, Alyssa runs generate-key-system-parameters to generate a value for p and g, and then broadcasts them to Ben. Ben then uses them as input to create-key-system which picks a random number x and computes y=gx modulo p to create a key system for Ben. Alyssa similarly uses create-key-system to create her own key system, also based on the same p and g.

The procedure choose-random used here takes an arbitrary integer n and returns a number chosen at random between 2 and n-2, inclusive. Picking random numbers in this range will be useful for several of the procedures in this problem set.

The procedure make-key-system in the final line of the procedure is another example of a data constructor. As with message-MAC pairs, we can select the individual pieces of a key system by using the data selectors: get-key-system-p, get-key-system-g, get-key-system-x, and get-key-system-y.

Once we have a key system, we can extract the public parts to form the corresponding published key: 

(define (key-system->published-key key-system)
  (make-published-key (get-key-system-p key-system)
                      (get-key-system-g key-system)
                      (get-key-system-y key-system)))

Here make-published-key is another data abstraction we have provided for you, with selectors get-published-key-p, get-published-key-g, and get-published-key-y.

Once values for p and g are agreed upon, Alyssa and Ben are now able to each create their own published-keys and exchange them with each other. It will be your task to define a procedure called compute-shared-secret-key which takes as input one party's key system and the other party's published-key and computes the shared key K.

Message Confidentiality

Now Alyssa is able to verify that messages sent by Ben are indeed sent by Ben. But let's say that Ben would prefer to keep the contents of his message secret, so that no one besides Alyssa can read its contents. His message now is: "Okay to let Dan Glen F Frince access the top secret design plans that no one is supposed to know we have finished".

Until recently, the only thing Ben could do was encrypt the message with some sort of encryption algorithm (that has a corresponding decryption algorithm that Alyssa could use to decrypt the message). However, with a method developed by Ron Rivest called ``Chaffing and Winnowing''10, Ben can attain message confidentiality without the need for any encryption at all. One advantage is that this technique then is not subject to any of the cryptographic export laws on encryption.

Chaffing and winnowing can be used to attain confidentiality. The idea is to break up the original message into several portions. A sequence number is assigned to each portion and a MAC is computed for each portion, so that one possible fragmentation of Ben's message might be: 

(1, "Okay to let",88113745325152792377081518730825748685)
(2, "Dan Glen F Frince",298000073913541298576002107633599888579)
(3, "borrow", 1134959076122225561497084604762542399)
(4, "the laptop",158229469958922351821566817068133464882)
(5, "at 9pm",243288456319990778564459053466932543310)
(6, "tonight.",122065247107374466114789321520482746691)

Counterfeit message-MAC-pairs called ``chaff'' are then introduced. These messages have MACs that are just random numbers so that they would fail the verify-MAC check. For example, Ben's message with chaff added might become: 

(1, "Okay to let",88113745325152792377081518730825748685)
(1, "Don't let",  816734537705403449034601635230275145533)
(2, "Jim Shooze", 90385953833903221289864436540546992276)
(2, "Dan Glen F Frince",298000073913541298576002107633599888579)
(3, "return", 231212365228026915476703335747869866170)
(3, "borrow",     1134959076122225561497084604762542399)
(4. "the car", 950183541258206532053995756202145128305)
(4, "the laptop", 158229469958922351821566817068133464882)
(5, "at 9pm",243288456319990778564459053466932543310)
(5, "before 7pm", 376911973028858680665155047229529071630)
(6, "tonight.",122065247107374466114789321520482746691)
(6, "tomorrow.", 60883900468057673564479753807402535694)

Only Alyssa who knows K can figure out which of the message-MAC pairs are authentic. This winnowing process allows Alyssa to efficiently weed out the chaff, while any other person not knowing Kwould be faced with a combinatorially intensive task should he desire to reconstruct Ben's message by considering all possible arrangements. In this manner, the contents of Ben's message is obscured and kept confidential without the use of any encryption technique.11

3. Tutorial exercises

You should prepare these exercises for oral presentation in tutorial.

Tutorial exercise 1:

Do exercise 1.3 of the text which asks you to define a procedure that involves the summing the squares.

Tutorial exercise 2:

Do exercise 1.26 of the text which looks at a less efficient variation of expmod.

Tutorial exercise 3:

Write the procedures choose-safe-prime and find-generator, which you will need for completing the computer part of this assignment. Choose-safe-prime should take a digits input (as does choose-prime, but note that digits will be the size of the generator and not the prime) and return a safe prime. Find-generator should take a safe prime and return a generator for the prime. Hint: make use of procedures we have already defined you! Bring your written answers to tutorial; your tutor will help debug your coding style and suggest alternatives.

4. Programming assignment

Begin by loading the code for problem set 1, using the Edwin command M-x load problem set.

Note on debugging procedures that use randomness: Some of the procedures you will be working with this assignment depend on selecting random numbers, and so will give different answers each time you run them. Such procedures can be confusing to debug, since it's hard to tell whether things are changing due to your modifications or just due to selecting different random numbers. To help you in debugging, we've provided a procedure reset-random! (which takes no arguments). Whenever you run (reset-random!) the random number generator will be returned to its initial state. This permits you to do repeatable experiments.

Computer exercise 1:

Implement the verify-MAC procedure, which takes as arguments a message-MAC-pair and a shared key, and tests if the value of the MAC is correct. For testing your procedure, we've provided two message-MAC-pairs mMAC1-ex-1 and mMAC2-ex-1 and a shared key skey-ex-1 which was the correct key used in generating only one of these two MACs. Turn in a listing of your procedure and demonstrate that only one message is authentic.

Computer exercise 2:

In this exercise, you will work with procedures that take as input a string message, a numerical key and an integer n, and outputs MAC that is the result of applying the MAC algorithm n times. For example, if n=3, the MAC is computed as: MAC(key $\oplus$ MAC( key $\oplus$ MAC (key $\oplus$ message))) where $\oplus$ represents string concatenation.

Consider the following recursive code: 

(define (recursive-compute-MAC string key times)
  (if (= 1 times)
    (compute-MAC sting key)
    (compute-MAC (recursive-compute-MAC string (- times 1)) key)))

(Note that compute-MAC has been specially designed to handle either strings or number versions of strings, so you do not have to worry about converting your MAC from a number to a string.)

If you try to evaluate: (recursive-compute-MAC "I hope this works" 87193 2) you'll get an error message. Use the debugger to help you figure out what is wrong with the code and make a note of the error messages that it gives you. A tutorial on the debugger is included at the end of this problem set. Once you have debugged the code, type in the correct definition and check that the MAC for "I hope this works" with key 87193 is: 163054733316285507945076193372690511037. Hand in the code for the correct recursive version and a transcript of your debugging session.

Implement iterative-compute-MAC, the iterative version.

Once you have working recursive and iterative versions, use trace which enables you to trace through each recursive call. For example, type (trace recursive-compute-MAC) to initiate tracing of this procedure. For the iterative version, you can trace a procedure that is defined within another procedure by typing, for example, (trace iterative-compute-MAC '(iter)) if iter was the name of the internal helper procedure that you defined within iterative-compute-MAC.

Select some message, key and n, and demonstrate the difference between recursive and iterative processes by tracing the execution of each procedure given the same inputs.

Computer exercise 3:

Define the procedures choose-safe-prime and find-generator, which you wrote for one of the tutorial exercises Test them by finding a safe prime (use size equal to 5) and a generator for it. Once this is working, you should be able to run the procedure generate-key-system-parameters in order to do the next exercise.

Computer exercise 4:

Implement the compute-shared-secret-key procedure for the Diffie Hellman key exchange. Using your code from exercise 3, show how to generate a key system (use size equal to 5) and a published key system for Alyssa and for Ben, and also show how Alyssa is able to compute the shared secret key given her key-system and Ben's published key.

Computer exercise 5:

To see how chaffing and winnowing works, we've provided you with some message-MAC-pairs. The original message was broken up into 5 fragments, and chaffing was introduced so that there are three message possibilities for each of the five sequence numbers. Thus, the three possible messages for the first fragment (sequence number 1) are seq1-poss1-ex-5, seq1-poss2-ex-5 and seq1-poss3-ex5. The possible messages for the other sequence numbers are named similarly (seq2... and so on).12 We've also provided the shared key that was used to compute the valid MACs: skey-ex-5.

(a) Find the final message by assembling only those fragments that have a valid MAC.

Now, let's look at what someone other than Alyssa and Ben has to do if they want to try to figure out the original message.

Let r be the number of fragments the message is broken up into, and let s be the number of possibilities for each fragment (for Computer exercise 5, r=5 and s=3).

(b) For someone not knowing the shared key K, how many possible complete messages would he/she have to consider? (A complete message is one where you have to choose one of the s possible messages for each of r sequence numbers). Express your answer in terms of r and s.

(c) For someone not knowing the shared key K AND not knowing the sequence numbers of each fragment possibility, (so that he/she simply gets rs message-MAC-pairs), how many possibilities would there be now?

(d) For someone not knowing the sequence numbers, but possessing knowledge of K, how many possibilities are there?

Computer exercise 6:

Write a procedure find-discrete-log that takes as arguments values for y, g, and p, and returns an x such that $y \equiv g^x \bmod p$ by trying all possible valid values for x. Once this has been defined, you should be able to run the supplied procedure crack-published-key that cracks a published key, returning the original key system. Test your procedure by cracking the published key pk-ex-6 which is predefined in this problem set to be p=19079, g=362, y=6843.

How long did it take? To help you determine this, we've included a procedure called timed, which, if you place at the beginning of a combination, will evaluate the rest of the combination (as if the timed weren't there) and return the value along with the time required for the evaluation. Thus, evaluating 

(timed crack-published-key pk)
will apply the procedure crack-published-key to the argument pk (or whatever argument you want to use) and return the result, together with the time (in seconds) required to do the computation. Find the amount of time it takes to crack pk-ex-6.

Crack some public keys of size 5. Remember that all the random choices will result in a wide range of results, but you should be able to get some sort of average time.

Suppose you had a million times the computational resources that you are now using in working on this problem set, and that all these resources could be dedicated to cracking a single key. If you can expect the time to crack a key to increase by a factor of 10 for every digit added, how long would it take to crack a key of size 50? Of size 100? Give your answer in seconds, minutes, days, or years, whichever seems most appropriate.


Turn in answers to the following questions along with your answers to the questions in the problem set:

1.
About how much time did you spend on this homework assignment? (Reading and preparing the assignment plus computer work.)

2.
Which scheme system(s) did you use to do this assignment (for example: 6.001 lab, your own NT machine, your own Win95 machine, your own Linux machine)?

3.
We encourage you to work with others on problem sets as long as you acknowledge it (see the 6.001 General Information handout).

Debugging Tools

During the semester, you will often need to debug programs. This section will acquaint you with the debugger. Additional information can be found in Don't Panic, and by typing ? in the debugger.

The Debugger

Type the following two define statements into your *scheme* buffer, and evaluate each of them. 

(define p1
  (lambda (x y) (+ (p2 x y) (p2 x))))

(define p2
  (lambda (z w) (* z w)))

Next, type and evaluate the expression (p1 1 2). This should signal an error, with the message: 

;The procedure #[compound-procedure P2] has been called with 1 argument
;it requires exactly 2 arguments.
;Type D to debug error, Q to quit back to REP loop:

Don't panic. Beginners have a tendency to quickly type Q, often without even reading the error message. Then they stare at their code in the editor trying to see what the bug is. Indeed, the example here is simple enough so that you probably can find the bug by just reading the code. Instead, however, let's see how some helpful information about the error can be produced.

First of all, there is the error message itself. It tells you that the error was caused by a procedure being called with one argument, which is the wrong number of arguments for that procedure. Unfortunately, the error message alone doesn't say where in the code the error occurred. In order to find out more, you need to use the debugger. To do this type D to start the debugger.

Using the Debugger

The debugger allows you to examine pieces of the execution in progress, in order to learn more about what may have caused the error. When you start the debugger, it will create a new window showing two buffers. The bottom buffer right now is empty, and the top buffer should look like this: 

     COMMANDS:   ? - Help   q - Quit Debugger   e - Environment browser
This is a debugger buffer:
Lines identify stack frames, most recent first.
   Sx means frame is in subproblem number x
   Ry means frame is reduction number y
The buffer below describes the current subproblem or reduction.
-----------
The *ERROR* that started the debugger is:
  The procedure #[compound-procedure 6 p2] has been called with 1 argument;
  it requires exactly 2 arguments.



>S0  (#[compound-procedure 6 p2] 1)
    R0  (p2 x)
 S1  (p2 x)
    R0  (+ (p2 x y) (p2 x))
    R1  (p1 1 2)
 --more--

You can select a frame by clicking on it with the mouse or by using the ordinary cursor line-motion commands to move from line to line. Notice that the information bottom buffer changes as the selected line changes.

The frames in the list in the top buffer represent the steps in the evaluation of the expression. There are two kinds of steps--subproblems and reductions. For now, you should think of a reduction step as transforming an expression into ``more elementary'' form, and think of a subproblem as picking out a piece of a compound expression to work on.

So, starting at the bottom of the list and working upwards, we see (p1 1 2), which is the expression we tried to evaluate. The next line up indicates that (p1 1 2) reduces to (+ (p2 x y) (p2 x)). Above that, we see that in order to evaluate this expression the interpreter chose to work on the subproblem (p2 x) which produces the error because two arguments are required.

Take a moment to examine the other debugger information (which will come in handy as your programs become more complex). Specifically, in the top buffer, select the line

>S1  (p2 x)

The bottom buffer should now look like this: 

                         SUBPROBLEM LEVEL: 1
Expression (from stack):
 Subproblem being executed highlighted.
    (+ (p2 x y) (p2 x))
---------------------------------------------------------------------
ENVIRONMENT named: (student)
    has 68 bindings (see editor variable environment-package-limit)

==> ENVIRONMENT created by the procedure: P1
      x = 1
      y = 2
---------------------------------------------------------------------
;EVALUATION may occur below in the environment of the selected frame.

The information here is in three parts. The first shows the expression again, with the subproblem being worked on highlighted. The next major part of the display shows information about the environments. We'll have a lot more to say about environments later in the semester, but for now notice the line

==> ENVIRONMENT created by the procedure: P1

This indicates that the evaluation of the current expression is within procedure p1. Also we find the environment has two bindings that specify the particular values of x and y referred to in the expression, namely x = 1 and y = 2. At the bottom of the description buffer is an area where you can evaluate expressions in this environment (which is often useful in debugging). For example, try evaluating (+ x y), and notice that you can do this, even though these values of x and y are ``local'' to this activation of P1.

Before quitting the debugger try to continue to scroll down through the stack past the line: R1 (p1 1 2) (you can also click the mouse on the line -more- to show the next subproblem). You will then see additional frames that contain various bits of compiled code. What you are looking at is some of the guts of the Scheme system--the part shown here is a piece of the interpreter's read-eval-print program. In general, backing up from any error will eventually land you in the guts of the system. (Yes: almost all of the system is itself a Scheme program.)

You can type q to return to the Scheme top level interpreter.

The Stepper

The stepper is another useful debugging tool that you should become acquainted with. Go into the Scheme buffer and type the expression (+ (* 3 4) (* 5 6)), but instead of evaluating it with c-X c-E, type M-s. The screen will split to show two windows. The top is your Scheme buffer; the bottom is the Stepper buffer, which right now should read,

(+ (* 3 4) (* 5 6)) => ;waiting
``Waiting'' means that it's waiting for you to tell it to go on, which you do by pressing the space bar. You'll see Scheme start to work on the subexpression (* 5 6). Continuing to press the space bar will show each element in the evaluation. The various ``waiting'' tokens will be replaced by the values as the evaluation proceeds. At the end, you should be up at the top of the window again, with 42 shown as the value of the call to the stepper. At this point, you can get out of the stepper by moving back to the Scheme buffer.

Try stepping this same expression a few times until you see clearly what is going on. Rather than always hitting the space bar, there are a couple of other stepper commands you can try (press ? to see them listed):

If you were to try stepping through the evaluation of (p1 1 2), which is the expression you used above to learn about the debugger, you will find that when you get to the evaluation of the expression that produces the error, you'll see #[some-unspecified-return-value] as the result--this should give you a hint that something has gone wrong.

In general, you use the debugger and stepper to home in on bugs from two different ``directions.'' If you have a program that signals an error, you can just let the error occur and use the debugger to try to figure out what happened; or you can step through the program up to the point where you see the error happen and try to figure out what is causing it.

Debugging can be frustrating. The debugging tools are your friends. Call on them regularly!

About this document ...

This document was generated using the LaTeX2HTML translator Version 98.1p1 release (March 2nd, 1998)

Copyright © 1993, 1994, 1995, 1996, 1997, Nikos Drakos, Computer Based Learning Unit, University of Leeds.

The command line arguments were:
latex2html ps1-crypto.

The translation was initiated by Duane Boning on 1998-09-08

next up previous
Duane Boning
1998-09-08