The vector cross product also acts on two vectors and returns a third vector. Geometrically, this new vector is constructed such that its projection onto either of the two input vectors is zero.

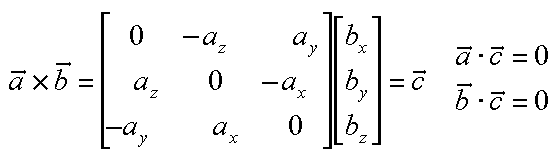
In order for one vector to project onto another with a length of zero, it must either have a length of zero, or be perpendicular to the second vector. Yet the vector generated by the cross-product operator is perpendicular to two vectors. Since the two input vectors define a plane in space, the vector that results from the cross product operation is perpendicular, or normal to this plane.

For any plane there are two possible choices of a normal vector, one on each side of a plane. The cross product is defined to be the one of these two vectors where the motion from the tip of the first input vector to the tip of the second input vector is in a counter-clockwise direction when observed from the side of the normal. This is just a restatement of the right-hand rule that you are familiar with.