 |
By hiding the previously-exposed implementation details of barrier synchronization and process communication from the programmer, the new BSP programming interface makes it much easier to write Bayanihan applications than before. At present, we have successfully used it not only to rewrite existing applications in a more readable and maintainable SPMD style, but also to implement new programs and algorithms such as Jacobi iteration, whose more complex communication patterns were difficult to express in the old model.
Unfortunately, while it is now possible to write a much wider variety of parallel programs with Bayanihan, such programs may not necessarily yield useful speedups yet since the underlying implementation is still based on the master-worker model. For example, even though one can now use peer-to-peer style communication patterns in one's code, these communications are still sequentialized at the implementation level since they are all performed by the central server. Also, since all work objects are currently checkpointed at the end of each superstep (i.e., workers send back their entire process state to the server at each bsp_sync()), algorithms that keep large amounts of local state between supersteps will perform poorly as this state would be unnecessarily transmitted back and forth between the server and the worker machines.
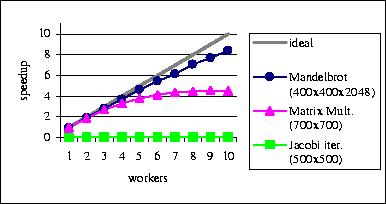
Figure 8 shows speedup results from some tests using 11 200 MHz Pentium PCs running Windows NT 4.0 on a 10Mbit Ethernet network, with Sun's JDK 1.1.7 JVM on the server and Netscape 4.03 on the 10 clients. The Mandelbrot test is a BSP version of the original Bayanihan Mandelbrot demo running on a 400x400 pixel array divided into 256 square blocks, with an average depth of 2048 iterations/pixel. The matrix multiplication test is a variation of the sample code in Sect. 4.2 where the worker processes get 10 rows of A at a time to improve granularity, and do not get C from the main work. It was run using 700x700 float matrices. The Jacobi iteration test solves Poisson's equation on a 500x500 double array decomposed into a 10x10 2D grid, with an exchange of border cells and a barrier synchronization done at the end of each iteration.
As shown, the ``embarassingly parallel'' Mandelbrot demo performed and scaled reasonably well. In contrast, the much finer-grain Jacobi iteration test performed very poorly, being at best about 40 times slower than a pure sequential version. This is not so surprising, though, given that it takes less time for the server to compute an element than to send it to another processor. Although speedups are theoretically still possible if the array is very large and workers are allowed to keep ``dirty'' local state for a long time, we cannot expect to get any speedup in this case since work objects send all their elements back to the server at the end of each iteration. On a more positive note, the matrix multiplication test, which employs a master-worker-like communication pattern (although written as a message-passing program), performed much better than the Jacobi iteration test, though not as well as the Mandelbrot test. The limiting factor in this case was the time needed to send the matrix B to the worker clients. Since we currently do not support multicast protocols, the server has to send B to workers individually. Thus, the broadcast time grows linearly with the number of worker clients, and eventually limits speedup. In the future, it may be possible to improve performance by using a more communication-efficient algorithm. However, most such algorithms keep local state between supersteps, and will thus probably be inefficient in the current implementation.
These results show that at present, Bayanihan BSP is still best used with coarse-grain applications having master-worker style communication patterns, and more work needs to be done to improve performance and scalability in other types of applications. Meanwhile, however, simply allowing programmers to write much more complex parallel programs than before is already a major result in itself, and represents a significant step towards making Java-based volunteer computing systems useful for realistic applications.