| Fig. 21. Node types |
| (a) Fully Unaccounted Node |
 |
| (b) Fully Accounted Node |
 |
| (c) Partially Unaccounted Nodes |
 |
| This section is part of Patil, Ramesh S. Causal Representation of Patient Illness for Electrolyte and Acid-Base Diagnosis. MIT Lab for Comp. Sci. TR-267 (1981). |
This chapter deals with the operations for building causal models (called PSMs; the Patient Specific Models) that can explain a patient's illness. A PSM is created by instantiating portions of ABEL's general medical knowledge. The creation of a PSM requires establishing and maintaining a correspondence between the medical knowledge and the observations, so that the information from each source can be added together. Much of the meaning of an observation depends on the context provided by the PSM; conversely, the PSM is created by assimilating many observations. As the PSM is multi-level, this assimilation requires the ability to summarize a detailed description into aggregate global summaries and the ability to disaggregate a summary into detailed description. This can be achieved based on the observation that the cognitive maps can be organized around local landmarks (focal nodes described in the previous chapter). The local topology surrounding a landmark can be described relative to the landmark and the landmarks then related to each other to construct the next level summary. It is possible to maintain sufficient mapping between adjacent levels for efficient use of this map for problem solving, if the summarization is carried out gradually using small steps, and in strict adherence to the principle of locality. Finally, note that detailed descriptions are likely to be much more accurate than global ones; detailed physiological descriptions tend to be much more accurate than global syndromic descriptions. Furthermore, local inconsistencies are easy to detect and correct, and are usually attributed to particular observations. Global inconsistencies, however, are much more difficult to pin down and are usually due to systematic errors in the interpretation of local observations and unwarranted extensions of local observations. Therefore, in building the PSM we interpret observations at the most detailed level possible and resolve inconsistencies arising at an aggregate level by using more detailed levels.
A PSM is a multi-level causal model, each level of which attempts to give an account of the program's understanding of the patient's case. Each PSM contains all the diseases and findings that have been observed or concluded in a given patient along with hypothesized diseases, findings, and their interrelationships, which together form a coherent explanation. Within each PSM, the known and hypothesized diseases, findings and their interrelationships are mutually complementary, while the alternate PSMs provide alternate explanations which are mutually exclusive and are competing to explain a patient's illness. Note that considering a PSM as a hypothesis for a patient's illness avoids the problem faced by the previous programs which considered each possible individual disease as a complete hypothesis, as discussed in chapter 1.
The PSMs are implemented using a Patient Specific Data structure (called PSD). The PSDs are organized in a tree. The PSD in the root position of the tree contains observed findings and the structure common to all the PSMs. Differing interpretations of the observed findings are described by creating inferior PSDs each containing incremental changes (additions as well as deletions) to their superior PSD. Each PSD in the tree inherits from its superiors all the structure present in them except that which is explicitly deleted.17 The structure visible from each leaf node of the PSD tree corresponds to an individual PSM. The list of PSMs at any given instant of diagnosis is called causal hypothesis list (CH-list).
Each PSD is implemented as a record structure containing a record for each level of description, a list of deleted elements and a pointer to the superior PSD containing it. The record structure of a PSO is:
(<level-0>,<level-l>,<level-2>,<level-3>,<level-4>,<deleted-elements>,<superior>)
The description of each level is implemented as a record structure consisting of a set of nodes, a set of links describing the relations between the nodes at the given level, and two sets of focal links connecting the description at the current level to the description at the adjacent lower and upper levels. The record structure of a level is:
(<nodes>, <links>, <focal-links up>, <focal-links down>)
The tree structure of the PSDs allows different PSMs to share structure common between them, providing efficiency in storage as well as in comparison of the structures of different PSMs. All the new information received is always added to the root PSD, the PSD common to every PSM. However, if this new information can be explained in more than one way in the context of a given PSM, the leaf PSD corresponding to the PSM is expanded to represent each of these explanations separately.
The PSMs are created and augmented using structure building operations described in this section. These operations are initial formulation to create the initial set of PSMs from the presenting complaints and lab results, aggregation to summarize the description at a given level of detail to the next more aggregate level, elaboration to disaggregate the description at a given level to the next more detailed level, projection to hypothesize associated findings and diseases suggested by states in the PSM, and constituent summation and decomposition to evaluate the combined effects of multiple etiologies and to evaluate the unaccounted components of partially accounted findings.
One of the most startling observations uncovered from the study of clinical problem solving is the physician's response to the presenting complaints [Pauker76, Elstein77, Kassirer78].
“The most striking aspect of the history-taking process revealed by the protocols is the sharp focus of the clinicians' problem-solving behavior. The subjects generated one or more working hypotheses early in the history-taking process when relatively few facts were known about the patient. At a time when the clinician was aware only of the age, sex, and presenting complaints of the patient, he often immediately introduced a hypothesis, ...“The process of hypothesis activation dominated the early part of the diagnostic session as the physicians searched br some explanation of the findings and for a context in which to proceed. Later in the session the emphasis was on hypothesis evaluation rather than hypothesis activation.”
— Clinical Problem Solving [Kassirer78, pages 249-250]
It is useful for a program to separate, like clinicians, the initial formulation of the diagnostic problem from subsequent revisions in the diagnostic alternatives. The patient specific information available at the initial phases of diagnosis is generally limited to a few nonspecific complaints. It does not provide sufficient context for a data-driven problem solver designed to perform optimally during later stages of diagnosis. Thus, failure to recognize the differences between the initial and the subsequent stages of diagnosis may result in an unfocused diagnostic inquiry with many irrelevant questions until sufficient information can be gathered for establishing a context for an orderly inquiry. The program presented here makes such a distinction. However, substantial improvement in the initial formulation of the diagnostic problem will be required before this distinction can be effectively exploited.
When provided with the initial findings and a set of serum electrolyte values, ABEL constructs a small set of PSMs, using the following steps. First, it analyses the electrolytes and formulates the possible single or multiple acid-base disturbances that are consistent with the electrolyte values provided. It then selects from them a small set which is consistent with the initial findings. Next, it generates a pathophysiological explanation of the electrolytes based on each of the proposed acid-base disturbances. This is achieved by elaborating known clinical information to the pathophysiological level, where its relationships to the laboratory data is determined by projecting the unique causes and definite consequences of every node. The program then summarizes these pathophysiological descriptions to the clinical level by repeated application of the aggregation operations. This process results in the initial description of the patient being built at every level of detail. These descriptions form the program's initial hypotheses, and are later modified as new information becomes available. Note that each of the mechanisms, aggregation, elaboration and projection are used in the initial formulation of the PSM.
This section introduces the naming conventions and definitions for describing types of nodes and their internal structures in a PSM.
| Fig. 21. Node types |
| (a) Fully Unaccounted Node |
 |
| (b) Fully Accounted Node |
 |
| (c) Partially Unaccounted Nodes |
 |
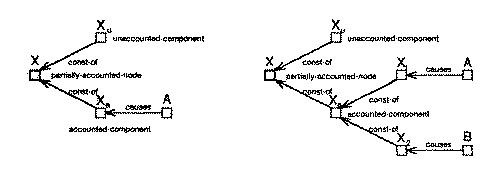
Some of these structures are also illustrated in figure 21. Figure 21(a) shows a fully unaccounted node X. Figure 21(b) shows three possible structures for fully accounted nodes. The first structure shows a fully accounted node X and its cause A. The second and third structures show a fully accounted node X with two causal predecessors A and B which together account for X. In the third structure X is a primitive node and therefore the components of X (i.e., X1 and X2) accounted for by each of its causes are explicitly instantiated. However, in the second structure X is a fully accounted for composite node, therefore, A and B are directly connected to X suppressing the component structure present at the greater levels of detail. Figure 21(c) shows two possible structures for partially accounted node X. X is decomposed into an accounted component Xa, and an unaccounted component Xu. Xu is an unaccounted node with structure similar to case (a) and Xa is a fully accounted node and has structure similar to case (b).
The aggregation process is used to summarize the description of the patient's illness at a given level to the next more aggregate level. This summarization of the causal network is achieved by identifying nodes (called focal nodes) which can serve as landmarks, summarizing each focal node and its surrounding causal relationships at the next more aggregate level (called focal aggregation), and by summarizing the chain of causal relations between nodes by a single causal relation between the initial cause and the final effect nodes (called causal aggregation).
In aggregating a causal network we must first identify the nodes that form the focal points around which the causal phenomenon can be summarized. Consider a partially-constructed PSM in which some nodes at a detailed level have been instantiated. A node is a focal node if the following three conditions are satisfied. (1) In the medical knowledge-base this node is the locus of the elaboration structure of at least one node at the next more aggregate level. (2) In the PSM at least one such higher level node already exists, or can be instantiated. (3) The aggregation is not inconsistent with the existing structure of the PSM. If the aggregate node does not exist, then both it and the focal link are instantiated, If the aggregate node exists, the focal link connecting the two is instantiated and the profiles of the focus and the aggregate nodes are updated using any additional Information that can be inferred by this connection. Finally, if more than one possible candidate for aggregation is consistent with the causal structure above, the focal aggregation process is deferred until additional information can be obtained to resolve this ambiguity.
Once we have determined the focal aggregations for nodes at a given level of detail we need to determine the causal relations among these aggregate nodes. This is achieved using causal aggregation. The process of causal aggregation takes a node and its causes and aggregates the relation between them according to one of three rules. First, if the node has no causal predecessors or if none of the causal paths leading into the node (predecessor paths) have an aggregable node, then the focal aggregation of the node does not have any causal predecessors. The focal aggregation node then is either an ultimate etiology or is an unaccounted node and no new edges need to be added to the aggregation. Figure 22 shows two examples of causal aggregation of fully unaccounted nodes. The first example shows causal aggregation of low- serum-K-1. Focally aggregating we instantiate hypokalemia-1. Next, we follow the predecessor path of low-serum-K-1 in search of an aggregable node. As low-total-ecf-K-1 and K-loss-1 are not aggregable nodes, this search fails, and no additional structure is created. However, as the predecessor path terminates in an unaccounted node, the focal aggregation of low-serum-K-1, hypokalemia-1, is marked unaccounted. The second example shows high-serum-Cl-1. As high- serum-Cl-1 does not have any predecessor, its focal aggregation, hyperchloremia-1, does not have any causal predecessor. Furthermore, as high-serum-Cl-1 is unaccounted, hyperchloremia-1 is also unaccounted.
Second, if every predecessor path has a node with a focal aggregation then the focal aggregation of the node is fully accounted for. The causal aggregation is achieved by creating a causal link between the focal aggregation of the node and the first focal aggregation in each path. Figure 23 shows two examples of causal aggregation of fully accounted nodes. In the first example the low-serum-K-1 has one predecessor path and that predecessor path contains an aggregable node, lower-GI-loss-1. Therefore, low-serum-K-1 is a fully accounted node, and its causal aggregation is achieved by focally aggregating lower-GI-loss-1 and causally connecting hypokalemia-1 to it. In the second example, low-serum-K-1 has two predecessor paths, each containing an aggregable node. The causal aggregation is achieved by focally aggregating each of these two aggregable nodes and then causally connecting hypokalemia-1 to them as shown.
Finally, if only some of the predecessor paths have nodes with focal aggregations then the focal aggregation of this node is partially accounted for. The causal aggregation is achieved by decomposing the node into two components: (1) the accounted component, due to paths which have some focal aggregation, and (2) the unaccounted component, due to paths that do not. The focal aggregation of the node is then decomposed based on the decomposition at the present level and the two cases are treated as described above. Any new information that can be derived from the addition of causal links in the PSM is used to update the profiles of nodes involved in aggregation. Figure 24 shows an example of causal aggregation of a partially accounted node. In this example one of the two predecessor paths of low-serum-K-1 contains an aggregable node, lower-GI-loss-1, we focally aggregate this node. The other predecessor path terminates in K-loss-3, an unaccounted node. Next, we compute the component of low-serum-K-1 that can be accounted for by lower-GI-loss-1 and the component that remains unaccounted for because of the unaccounted K-loss-3. Then we compute the mapping of these two components at the next level of aggregation and instantiate hypokalemia-2 (the component accounted for by lower-GI- loss-1) and hypokalemia-3 (due to unaccounted K-loss-3). We then causally connect hypokalemia-2 to lower-GI-loss-1 and mark the hypokalemia-3 as being unaccounted for.
Elaboration is the dual of the aggregation operation described above. It is used to disaggregate the description of a causal network at a given level to the next more detailed level. In other words, given a summary description of a causal phenomenon, it provides a more detailed description consistent with the summary. This is achieved by instantiating the focal description of each composite node (called focal elaboration) and by instantiating the causal pathway between these detailed nodes corresponding to each causal link at the aggregate level (called causal elaboration). If the causal pathway being instantiated interacts with other causal paths in the PSM, the combined effects of the multiple causality are computed using component summation. The combined effects of this summation can then be aggregated upwards to reflect the better understanding of the causal phenomenon at the higher levels of aggregation. This is one mechanism where two aggregate phenomena may become linked, through the interaction of their detailed descriptions.
In summary, the focal aggregation and elaboration create mappings between nodes across different levels, and causal aggregation and elaborations create mappings between causal links across different levels.
To elaborate a causal network we identify the nodes in the network that have been used as summary descriptions, establish their references at the next more detailed level, and establish additional nodes and links at the detailed level to describe the phenomenon described in the aggregate network. The operation of focal elaboration deals with the first two of the three steps mentioned above.
A node can be focally elaborated if it is a composite node, and if a node corresponding to its focus already exists or can be instantiated in the PSM. If the focus node does not exist, then both it and the focal link are instantiated. If the new node is inconsistent with the detailed level, the detailed level is modified to re-establish overall consistency. If the focus node exists and is consistent, then the focal link connecting the two is created and the profiles of the node and its focus are updated using any additional information that can be inferred by this symbiosis. Finally, if more than one possible candidate for focal elaboration is consistent with the causal structure above, the focal elaboration process is deferred until additional information to resolve this ambiguity can be obtained.
Causal elaboration is used to determine the causal relations between nodes at a detailed level based on the causal relations between the nodes at the next more aggregate level. Causal elaboration is centered around the composite causal link and the chain of causal links that describe each composite causal link. To elaborate a composite link, the program matches the causal path associated with the link, against existing paths in the PSM. If some part of this pathway is not present, the program recurs on each missing link in the pathway (starting from the focus node of the cause) until the link being elaborated is a primitive. When the link being elaborated is primitive it is instantiated under one of the following conditions.
The program also updates the profiles of the nodes in the causal pathway using any additional information that can be inferred by addition of the pathway. Finally, the aggregation operation is used to revise the description of the next more aggregate level to reflect the addition of the causal pathway.
This process is illustrated with the help of the simple example shown in figure 25. Let us consider a patient with hypokalemia and salmonellosis. For the example, let us also assume that by some reasoning process we have established a causal link between salmonellosis and hypokalemia. The elaboration operation can then be used to establish this relation at more detailed levels. The pre-existing structure in the PSM is shown in solid lines, the link being causally elaborated (between hypokalemia and salmonellosis) is shown in solid bold and the links added by the process of elaboration are shown in bold broken lines. The elaboration process attempts to match the causal path corresponding to the link between salmonellosis and hypokalemia at the next level of detail, namely, salmonellosis —causes—> lower-GI-loss —causes—> hypokalemia. The link between salmonellosis and lower-GI-loss already exists. However, the link between lower-GI-loss and hypokalemia does not and must be created and elaborated further. Similarly, at the next level, the link between lower-GI-loss and K-loss does not exist. As this link is primitive the recursion terminates with creation of this link. Furthermore, as the attributes of K-loss and lower-GI-loss are compatible and the two are causally consistent, this link can be established by simply adding its instantiation to the PSM. Having established this link the program aggregates this causal path to propagate the effects of the elaboration back to the higher levels of aggregation.
The projection operation is used to hypothesize and explain the associated findings and diseases suggested by the states in a PSM. The projection operation is very similar to elaboration. It differs from elaboration in that the causal relation being projected is hypothetical and therefore is not present in the PSM. Furthermore, the projection operation fails if the causal description of the hypothesized link is inconsistent with the description in the PSM at any level of detail. As a result, the application of the projection operation cannot result in the decomposition of a fully accounted node, creating an additional unaccounted component and therefore degrading the quality of explanation.
As stated above the projection operation is not an essential component of the structure building operations. However, it plays an important role in the diagnostic problem solver in exploring diagnostic possibilities, evaluating their validity and in generating expectations about the consequences of hypothesized diagnoses.
One of the important mechanisms in developtng an understanding of the patient's illness is the evaluation of the effects of more than one disease present in the patient simultaneously, especially when one of the diseases alters the presentation of the others. To deal with such a situation competently, the program must have the ability to identify the effect of each cause individually, and the ability to combine these effects together. In this section we present the component summation and decomposition operations. Component summation combines attributes of the components to generate the attributes of the joint node; component decomposition identifies the unaccounted component by noting differences between the joint node and its existing components. These operations enrich the PSM by instantiating and unifying component nodes when the case demands them. This occurs whenever multiple causes contribute jointly to a single effect. An important case of this arises whenever feedback is modeled, because in any feedback ioop there is at least one node acted on both by an outside factor and by the feedback loop itself. Finally, the decomposition of an effect with multiple causes into its causal components will also provide us with valuable information for evaluating the prognosis and formulating therapeutic interventions.
As the PSM is built, component summation and decomposition operations can cause a node in the program's general knowledge to be instantiated as a node and its several components in the PSM. If a node is primitive and there are multiple causes, the contribution of each cause is instantiated separately. Then the profile of the combination is computed using component summation. The combined effect is then instantiated and connected to its constituents by constituent links.
Because components are defined only for primitive nodes, the instantiation of composite nodes which involve component summation must be in terms of the summation of components in the node's elaboration structure. If the node is composite then we elaborate the constituent nodes around their focal nodes until we reach the primitive nodes associated with them. Then we combine these primitive nodes and aggregate their effects back. For example, if we know that a patient has hypobicarbonatemia and hypocapnia causing acidemia (figure 26), we can evaluate their combined effect as follows: (1) compute the component of acidemia caused by hypobicarbonatemia and hypocapnia individually, (2) focally elaborate these two components until each component can be described in terms of change in serum-pH (a primitive node), (3) sum the two components using component summation, and (4) aggregate the joint effect to derive the actual severity of acidemia.
| Fig. 27. Feedback loop represented using component summation |
 |
These operations deal not only with the magnitude of some disorder but also with other attributes such as duration. They are implemented by associating with each primitive node a multivariate relation that constrains the attributes of the node and its components. This mapping function is used by component summation in computing the attributes of the joint node from the attributes of the component nodes and by component decomposition in computing the attributes of the unaccounted component from the attributes of the joint node and its existing components. An example of the constraints is shown in the next example.
[(concentration~u electrolyte)
[union:u [value^u #c (combine-electrolyte-value*c
(value*c (value*u component:1)),
(value*c (value*u component:2)),
(default*c component:1))]
[start-time^u #c (min*c (value*c (start-time*u component:1)),
(value*c (start-time*u component:2)))]
[duration^u #c (max*c (value*c (duration*u component:1)),
(value*c (duration*u component:2)))]
[belief^u #c (min*c (value*c (belief*u component:1)),
(value*c (belief*u component:2)))]
[component:1 [value^u #c (component-electro1yte-value*c
(value*c (value*u union:u)),
(value*c (value*u component:2)),
(default*c union:u))]
[start-time^u #c (value*c (start-time*u union:u))]
[duration^u #c (value*c (duration*u union:u))]
[belief^u #c (value*c (belief*u union:u))] ]]
The above example describes the multivariate relation between the components and their summation for the concentration of electrolytes. This relation is divided into two parts; the first part (associated with slot “union:u”) describes procedures for combining the attributes of the two components (“compoņent:l” and “component:2”). In particular, it states that the value of the joint-state (union) is determined from the values of the two components and the default value of the electrolyte concentration using a lisp function “combine-electrolyte-value”. It further states that the belief in the joint-state is equal to the lesser of the beliefs in the components.18 Similarly, the “start-time” of the joint-node is the earlier of the two start times and the duration of the joint-state is the longer of the two durations. A similar set of procedures for computing the difference (component:1) between the joint-state and a given component state (component:2) is described in the second part of the example shown above. This mapping relation can be used for computing the component summation/decomposition of electrolyte concentrations in any one of the different fluids in the body such as extra-cellular fluid, intracellular fluid, and urine.
The component operations are activated when a node is added to the PSM where another node in the same class is already present. These operations incorporate the new node into the structure of the PSM and delete any structure in the PSM that is no longer valid due the the addition of the new node. These operations can be divided broadly into three cases based on the properties of the node already present and the new node being added: (1) both the new and pre-existing nodes are both unsupported by observation; (2) the new node being added is supported by observation and the pre-existing node is not; and (3) the new node is not supported by observation and the pre-existing node is. A node is said to be supported by observation if the node is either an observed node or is a causal predecessor of an observed node which is fully accounted for. The details of the three cases:
Case 1: Neither the new nor the pre-existing node is supported by observation. In this case the joint effect of the two nodes is computed and the two nodes are connected to the joint effect using component links. If the pre-existing node already has component structure, the new node is directly connected to the pre-existing joint effect and the attributes of the joint effect are revised to be consistent with this addition. Any of the successors of the two nodes which are consistent with the joint effect are rerouted through the joint effect and those which are not consistent are deleted and the effects of these deletions are propagated.
Case 2: The new node being added is supported by observation and the pre-existing node is not. In this case the joint effect of the resulting structure (upon application of the component operation) must be same as the new node. If the pre-existing node and the new node are consistent with one another then the pre-existing node is replaced with the new node and the operation is complete. If they are not, the difference between the observed and the unobserved is computed, and a node corresponding to the difference (called unaccounted-component) is instantiated. Next the pre-existing (accounted-component) node and the unaccounted component to the new (joint-effect) node are connected using component links. Any of the successors of the pre-existing node that are consistent with the joint-effect are rerouted through it and those that are not consistent are deleted and the effects of these deletions are propagated.
Case 3: The pre-existing node is supported by observation while the new node being added is not. As in the case 2, the observed node is the designated joint effect. This case is somewhat more complex, because the pre-existing node is observed and may have constituents of any possible form, i.e., may be fully accounted for, partly accounted for, or fully unaccounted for. In each case the new node is added to the pre-existing structure as a constituent as shown in the figure 28.
Figure 28 shows subcases of case 3 where the pre-existing node (bold square) is supported by observation while the new node (crossed square) being added is not. The left side of the figure shows the situation before the component summation and the right side shows possible situations after the component summation. Figure 28(a) shows the operation for a fully unaccounted pre-existing node. Figure 28(b) shows the operation for a fully accounted pre-existing node with one cause. The first structure on the right shows the situation when the effects of existing cause and the the new node are still consistent with the pre-existing node. In this situation the components of each of the two causes are instantiated and connected as shown in the figure. The second structure shows the situation when the sum of the new node and the effect of the existing cause is not consistent with the pre-existing node. In this situation the pre-existing node is decomposed into an accounted and an unaccounted component. The accounted component is dealt with similar to the first structure and the unaccounted component is marked as being unaccounted. Figure 28(c) shows the operation for a fully accounted pre-existing node with multiple causes. This case is handled similar to that in figure 28(b). Figure 28(d) and (e) show the operation for partially accounted pre-existing node. If the new node matches the unaccounted component of the pre-existing structure, the resulting structure is fully accounted for, if it does not the accounted and unaccounted components of the pre-existing node are recomputed and the new node is connected to the accounted components.
In this section we have developed a knowledge representation formalism and operations for dealing with effects with multiple causes and feedback loops common in the physiological regulation of the body's vital functions. The mechanism developed here is intended for symbolic description for reasoning with and explaining the abnormalities in physiological regulation in a patient, not for predicting the behavior of physiological parameters over time using dynamic simulation techniques.
This section is part of
The document was reconstructed for the Web in April 2002 by Peter Szolovits.Patil, Ramesh S. Causal Representation of Patient Illness for Electrolyte and Acid-Base Diagnosis. MIT Lab for Computer Science Technical Report TR-267. October 1981. Also: Ph.D. Thesis, MIT Dept. of Electrical Engineering and Computer Science.