Integrate-and-Fire
On Different Topologies
All-to-all networks, unfortunately, are not the bread and butter of amorphous computing. I started out, in order to see its behavior clearly, trying Peskin's algorithm on a line or ring (pictured below). A quick reminder about the spike train below: nodes which fire at the same time as at least one of their neighbors are shown in green, while nodes that fire alone are shown in blue. Also, since it is on a line, the nodes are in order and the representation is accurate. As you can see, synchronized regions form locally through absorptions, and eventually these regions merge together.
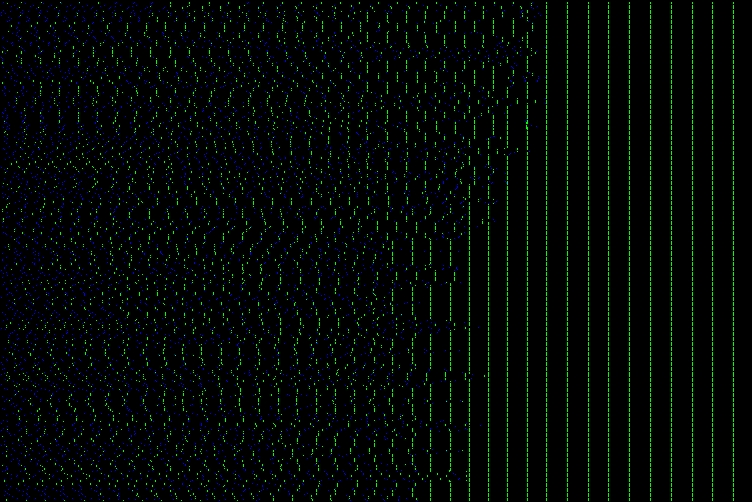
Why It Works
One would think that on the boundary of a region, an outside node would be able to "pick off" a node on the border of the region. The reason this is not the case is because of the pacemaker effect: say we have node A as the boundary node of a region (synchronized with that region) and node B its neighbor on the other side. When B fires, it advances A, so A fires sooner. If the coupling strength is large enough (there is a threshold somewhere between .0075 and .15, according to my simulations), then when node A fires, it will cause its neighbor inside its region to fire immediately and cause a chain reaction throughout the whole region. So the region stays synchronized. Indeed, if we decrease the coupling strength enough, we see regions form and break up seemingly endlessley. Similar behavior occurs on a lattice of two dimensions and on a random spatial distribution of nodes with nearest-neighbor coupling. These situations are both much easier to see in the direct representation. Again, it appears that the speed of synchronization depends on the connectivity of the network (in the sense of the number of connections to each node (its degree)). Analysis on anything more than all-to-all, unfortunately, is incredibly difficult because it requires going through increasingly many ranges of initial conditions as the number of nodes increases. It seems clear from extensive simulation that this will work in almost all initial conditions. Keep in mind that this only works in lagless situations.

