Towards a Programmable Material

Imagine a flexible substrate, consisting of millions of tiny interwoven programmable fibers, that can be programmed to assume a large variety of global shapes. Rather than build precisely engineered mechanical structures, a programmable material would allow one to program precise complicated structures starting from a single flexible mechanical base. Not only could one design many complex static structures by programming a single substrate, but also create dynamic structures that react to, and affect, the environment. For example, a flexible car surface that can change structure exactly at the point of impact, rather than having specifically engineered crumple points; an airplane wing that can dynamically change shape to resist shear; a programmable assembly line that can move objects around by producing ripples in specific directions; a reconfigurable robot that changes it shape based on what function it needs to perform; or a manufacturing line that replaces precise mechanical engineering with programming. Programmable materials would make possible a host of novel applications that blur the boundary between computation and the environment.

Biology, in particular morphogenesis, gives us many examples of complex structures formed from the cooperation of large numbers of cells. One example are epithelial cell sheets that can organize into complex structures such as branching tubes, neural folds and other structures through the actuation of many individual epithelial cells, each cell having limited force. Here we propose a model inspired by epithelial cell sheets - the programmable material is composed of identically programmed, connected, mechanical cells that organize into complex structures through the coordination of local shapes changes.

A Single Active Cell Odell, Oster, Alberch, and Burnside[1] present a mechanical model for how embryos form structures during neurulation and gastrulation, through the local deformations of epithelial cells. Each cell consists of fibers and contains a slightly compressible fluid. Apical (top) fibers can actively contract, and cause what is known as a purse string contraction. The cells are connected to each other and can cause invaginations when several neighboring cells contract. We use the cell model proposed by Odell et al, but allow all fibers to actively contract, or loosen. By programming the active fibers, one can create many simple shape changes - long columnar cells, short fat cells, triangular or conical cells. When these cells are connected together, many global shapes can be expressed, simply as compositions of these local shapes.

Various single cell deformations

Structures Composed of Active Cells

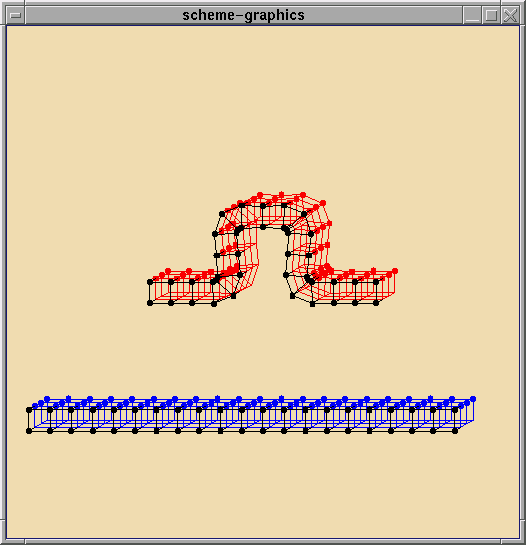
Structure I: A Ring of Active Cells

Each of these shapes can be described as simple local shape changes by individual cells. Combining this with simple pattern formation techniques (chemical tropisms, coordinate systems,etc) from amorphous computing, one can program the cells to coordinate to form the desired mechanical pattern.

Gastrulation and Ventral Furrow Formation: The first example approximates gastrulation in organisms such as a sea urchin. The active cells contract their apical and lateral fibers, with more contraction happening at the tip of the invagination. Eventually the invagination goes all the way through the body to form the gut. The second picture shows ventral furrow formation in drosophilia, where cells use apical contraction to form a tube on the ventral side of the cylinderical embryo (similar to example in [1]).
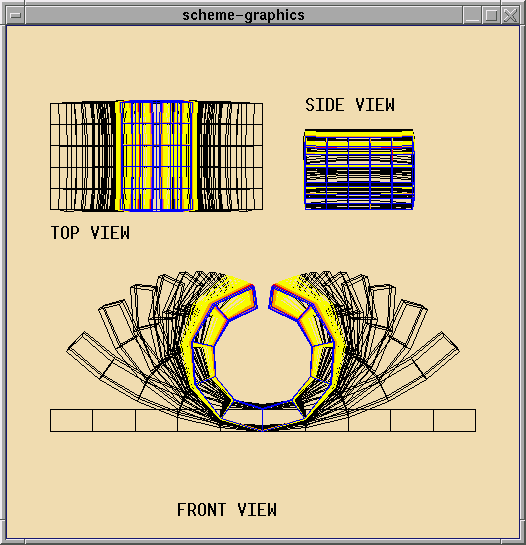
Cleaving into Two and the formation of Eyefolds: In a manner similar to gastrulation, the ring (or sphere) can form two smaller rings. This could represent the cleaving of a cell through the actions of fibers distributed in the cell membrane. The second example shows the formation of folds in the ring through alternating cells with apical contractions and basal contractions. Folds are common during development (chick cornea), however usually due to differential growth.
Bulb Formation, and Three fingers: Bulb formation is simply the opposite of ventral furrow. The fingers are also similar to bulbs, however with deepening invaginations (similar mechanisms to gastrulation) between the fingers.

Programming the Ring of Cells

The program for a cell consists of a unordered set of independent rules and each rule consists consists of a triggering event, a condition and actions. The state of a cell consists of boolean markers and timers.  Events consist of recieving a message from a neighboring cell, a marker whose timer expired or a sensor triggering. The condition is a boolean expression of markers. The possible actions are to affect the state, send a message, and set actuators. Underlying this language are gradients (see self-organising coordinate systems). that can be used to mark regions. All inter-cellular communication is through gradients.
 

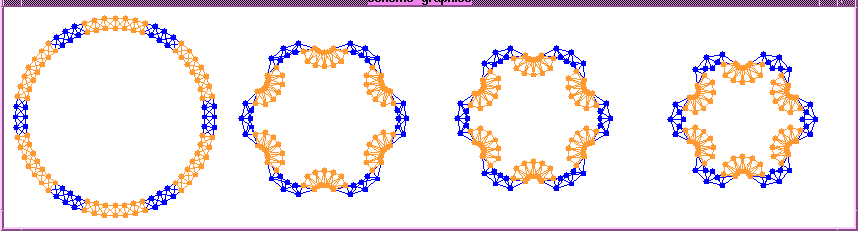
A Cell Program for Initiating Eyefolds: The result of this program is that folds (or invaginations) appear at random places on the ring with a separation of between 3 to 6 cells. The program uses the clubs algorithm (see publications), which uses short range inhibition to ensure that folds appear with some preferred spacing.  The program can be extended to cause cells close to the fold points to also contract their apical fibers. This program generates folds that are slightly different from this simulation example, where the folds are equidistant. The language currently does not have all the features necessary to implement general shapes. Other amorphous ideas, such as tropism, gradient slopes, etc can be added to allow one to express cell programs for all of the shapes mentioned above.

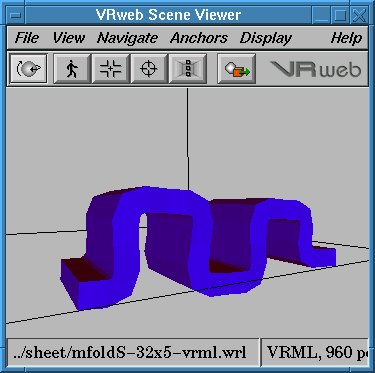
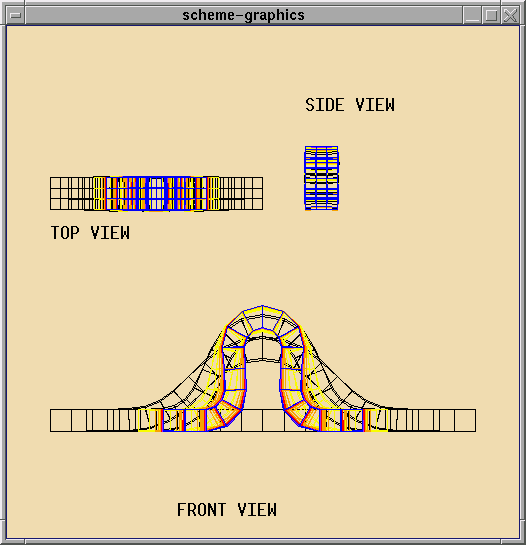
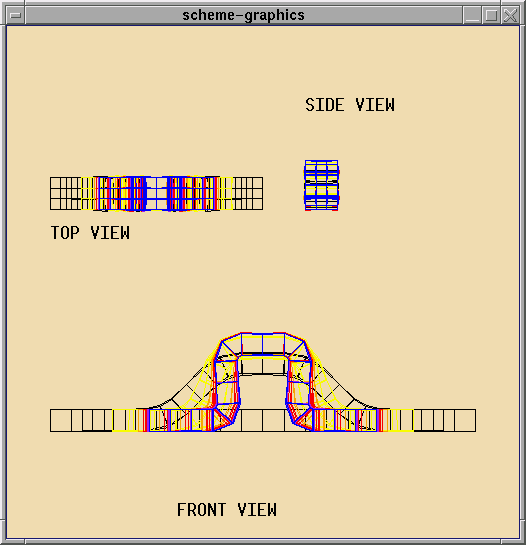
Structure II: A Sheet of Active Cells

References

[2] Amorphous Computing, H. Abelson, T. Knight and G. Sussman, white-paper Oct 1995.