...Cryptography
This problem set is based on an earlier 6.001 problem set originally written in 1987 by Ruth Shyu and Eric Grimson and revised in 1992 by David LaMacchia and Hal Abelson. There was a major revision by Hal Abelson for 1998 (changing the method of encryption from RSA to ElGamal). 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...cryptography.
The first publication of this idea appeared in W. Diffie and M. Hellman, ``New directions in cryptography,'' IEEE Transactions on Information Theory, IT-22:6, 1976, pp 644-654, and Diffie and Hellman have been credited with the invention. In December 1997, however, the British Communications Electronics Security Group (part of British intelligence), published a memo describing how the technique was invented by CESG's Malcolm Williamson in 1973, but kept secret. See James Ellis, ``The Story of Non-Secret Encryption,'' http://www.cesg.gov.uk/ellisint.htm. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...communicate
Note for those people familiar with the literature on cryptography: Alyssa P. Hacker and Ben Bitdiddle hold the patent on imaginary characters in 6.001. The management has accordingly notified Alice and Bob that they may not participate in this problem set. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
....
The notation tex2html_wrap_inline519 (read ``r is congruent to s modulo p) means that r and s produce the same value when they are reduced modulo p, i.e., that r and s have the same reminder modulo p. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...agreement
This method, and the digital signature method discussed below, are based on work during the early 80s by cryptographer Taher ElGamal. ElGamal currently works as a security expert for Netscape. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...g.
There's a bit of number theory we've sloughed over that guarantees that these algorithms are reasonable. Given a safe prime, the odds that a randomly picked g is a generator are about 1 in 2. Given a prime q, the odds that 2q+1 is also prime are about 1 in 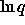tex2html_wrap_inline669. So trying random guesses is likely to succeed without too long a wait. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...primes:
We won't include the proof here, since this is not a number theory class. Just take the result on faith. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...text.
The particular symmetric cipher used here, Blowfish, was invented by cryptographer Bruce Schneier. We won't show you the code for this, which is buried in the guts of the Scheme system. For a description of the algorithm see Schneier's book Applied Cryptography, second edition, Wiley, 1996. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...problem.
Typical someones who come to mind here are certain government agencies, international crime rings, and MIT undergraduates. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...problem.
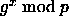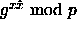Actually, if you're reading very closely, you'll see that we've made an unwarranted assumption. What you really need is to solve the so-called Diffie-Hellman problem: given tex2html_wrap_inline719 and tex2html_wrap_inline721, compute tex2html_wrap_inline723. As far as anyone knows, the only way to do this is to compute discrete logs, and for many classes of primes the discrete log problem and the Diffie-Hellman problem have been proved equivalent. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...fast.
As a consequence of this, the encryption you are implementing in this problem set really is a high-grade security method. For instance, the encryption system PGP 5.0 uses ElGamal encryption with a suggested prime size of around 300 digits. If anyone has the ability to crack something like that, they aren't talking. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...bad.
Note that when checking this condition we can compute each term modulo p before multiplying and comparing, because tex2html_wrap_inline811. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...result.
There are tremendous subtleties in designing a good message-digest function. One property it should have is that it should be computationally infeasible to find two strings that hash to the same value. The particular function used here, called MD5, was invented by Ron Rivest of MIT. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...night.
...with apologies to Baron Bulwer-Lytton and to Radia Perlman, Michael Speciner, and Charles Kaufman, who begin their outstanding book Network Security like this. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

Hal Abelson
Sun Feb 8 17:25:50 EST 1998