Quiz 1 - FT98 - Solutions
MASSACHVSETTS INSTITVTE OF TECHNOLOGY
Department of Electrical Engineering and Computer Science
6.001 -- Structure and Interpretation of Computer Programs
Quiz 1 -- Fall Term 1998
Closed book except for one sheet of notes (one side)
Print your name at the top of each page of this exam. We know this is
tedious, but prevents problems if the pages get separated.
Please write clear and concise answers to the questions posed in the
spaces provided in this booklet. You may use scratch paper if you
wish, but the spaces provided for the answers are the ONLY places we
will look at when grading the quiz. Your answers should be brief and
clear. The staff reserves the right to ignore illegible answers. In
grading problems that require programming, the staff will take into
consideration the style and clarity of your code, not just whether it
happens to produce the right result. Before starting, please check
that this booklet has all 11 pages (not counting this cover page, and
the list processing procedure definitions on the last page which are
provided for your convenience).
Print your name here:__Ben Bitdiddle______________________________
Print your tutor's name here:__Chuck Vest_________________________
Recitation instructor:__William Barton Rogers_____________________
If you have any comments about this quiz, please write them here:
Please do not write below this line -- reserved for administrivia.
_______________________________________________________________________
Problem Grade Grader Prob Grade Grader Grader's Comments
-------------------------------------------------- -----------------
| 1 | | || 4 | | |
--------------------------------------------------
| 2 | | || 5 | | |
--------------------------------------------------
| 3 | | || 6 | | |
--------------------------------------------------
--------------------------------------------------
| ||TOTAL | | |
--------------------------------------------------
----------------------------------------------------------------------
PROBLEM 1 (10 points)
A. Draw a box and pointer diagram for the value of z after the
following Scheme code is evaluated.
(define (make-two x)
(list x x))
(define z (make-two (make-two 3)))
ANS:
The key is to recognize that the first list produced by (make-two 3)
is *shared* in the second list:
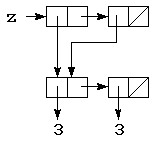
B. When z is evaluated, write what the interpreter prints:
z ==> ANS: ((3 3) (3 3))
----------------------------------------------------------------------
PROBLEM 2 (25 points)
Alyssa, Ben, Carl, and Dan argue that they can improve the
efficiency of the ENUMERATE-INTERVAL procedure from the book. Each of
their procedures (shown on the next page) work correctly. For each of
their procedures (as well as the procedure from the book also shown on
the next page) complete the table below to indicate:
A. Whether the procedure generates an iterative or recursive process.
B. The order of growth in space that the procedure requires (where we
count the maximum depth of deferred operations) as a function of n,
where n = hi - lo.
C. The order of growth in time that the procedure requires (where we
count the total number of CONS operations performed) as a function of n.
Definitions for the APPEND procedure, as well as the list handling
procedures LENGTH, MAP, ACCUMULATE, and FILTER are provided at the end
of this quiz handout.
| A. iterative | B. Space Needed | C. Time Needed |
| or recursive? | Theta( ) | Theta( ) |
------------------------------------------------------------------------
enumerate-interval | | | |
| recursive | n | n |
| | | |
------------------------------------------------------------------------
alyssa-ei | | | |
| recursive | n | n |
| | | |
------------------------------------------------------------------------
ben-ei | | | |
| recursive | n | n |
| | | |
------------------------------------------------------------------------
carl-ei | | | |
| iterative | 1 | n |
| | | |
------------------------------------------------------------------------
dan-ei | | | |
| recursive | n | n log n |
| | | |
------------------------------------------------------------------------
The hard one here was dan-ei. It is order n because the number of
deferred appends is order log_2 n, but when those finally get computed
each append "adds" order n deferred appends.
In time, append gets called about order log_2 n, and EACH of these
requires order n cons operations.
PROBLEM 2, Continued
(define (enumerate-interval lo hi)
(if (> lo hi)
nil
(cons lo (enumerate-interval (+ 1 lo) hi))))
(define (alyssa-ei lo hi)
(define (helper x)
(if (> x hi)
nil
(cons x (helper (+ 1 x)))))
(helper lo))
(define (ben-ei lo hi)
(cond ((= lo hi) (list hi))
((> lo hi) nil)
(else (cons lo
(cons (+ 1 lo)
(ben-ei (+ 2 lo) hi))))))
(define (carl-ei lo hi)
(define (helper x sofar)
(if (< x lo)
sofar
(helper (- x 1) (cons x sofar))))
(helper hi nil))
(define (dan-ei lo hi)
(let ((num (- hi lo)))
(cond ((> lo hi) nil)
((= num 0) (list lo))
((odd? num) (cons lo (dan-ei (+ 1 lo) hi)))
(else (let ((mid (+ lo (/ num 2))))
(append (dan-ei lo mid)
(dan-ei (+ 1 mid) hi)))))))
----------------------------------------------------------------------
PROBLEM 3 (25 points)
George (nicknamed the "Big Wave") goes to Las Vegas. He is
intrigued by one of the dice games, where n-sided dice (marked with
numbers from 1 to n on the sides) are being used. Exactly two dice
are always thrown, and George wants to build a list of the
combinations of the values shown on the two dice.
For example, at one table George finds that three-sided dice are
used, so the possible values are:
(DICE-COMBOS 3)
==> ((1 1) (1 2) (1 3) (2 1) (2 2) (2 3) (3 1) (3 2) (3 3))
Note that both (1 2) and (2 1) appear in the list, as George
wants to treat these as different combinations.
A. George first tries something simple in an attempt to produce the
above results:
(define (BUGGY-DICE-COMBOS n)
(let ((vals (enumerate-interval 1 n)))
(map (lambda (x) (list x n)) vals)))
Write the return value when George evaluates
(BUGGY-DICE-COMBOS 3)
==>
ANS: ((1 3) (2 3) (3 3))
B. Write the procedure DICE-COMBOS for George. The pairs of dice
combinations may appear in any order. You may also assume you have
the procedures ENUMERATE-INTERVAL, APPEND, LENGTH, MAP, FILTER,
and ACCUMULATE as shown on the last page of this quiz handout.
ANS: Many different ways this can be done. One simple way is
shown below (NOTE: this answer is REVISED 10/13/98 compared to
an earlier version posted in these solutions.)
(define (dice-combos n)
(let ((vals (enumerate-interval 1 n)))
(accumulate append nil
(map (lambda (a) (map (lambda (b) (list a b))
vals))
vals))))
Note that several solutions are very CLOSE, but depending on the
way the recursion occurs may fail to generate all the possible
dice combinations (e.g. may generate (1 3) but not also (3 1)).
George wants to use the list of dice combinations to calculate the
odds that the values of the two dice will sum to any given number, so
he will know how to place his bets to maximize his winnings (George is
known for his unrealistic optimism).
For example, in a 3-sided dice game (with the combinations shown
earlier), the odds of the sum being 4 are:
(FIND-ODDS-OF-SUM 4 3)
==> 0.3333 ; 3/9
since 3 combinations (1 3) (2 2) (3 1) out of 9 possible combinations
sum to 4.
C. Write the procedure FIND-ODDS-OF-SUM that takes two arguments: the
SUM and the number of sides N of the dice being used. Note that you
may use DICE-COMBOS even if you did not complete part B, as well as
any of the list procedures on the last page of this quiz handout.
ANS:
(define (find-odds-of-sum sum n)
(let ((combos (dice-combos n)))
(let ((matches (filter (lambda (combo)
(= sum (+ (car combo) (cadr combo))))
combos)))
(/ (length matches)
(length combos)))))
----------------------------------------------------------------------
PROBLEM 4 (14 points)
After each of the following Scheme expressions, print (or describe
if unprintable) the value resulting from evaluation of the expression.
If the expression results in an error, explain why.
A. (lambda (x) (/ y 0))
ANS: A PROCEDURE. (note that the body never gets evaluated, so
no error can occur.
B. ((lambda () 3.14159))
ANS: 3.14159
C. ((lambda (a b)
(if (odd? a)
(b 2)
(+ a b)))
4 6)
ANS: 10
D. (define f
(lambda (m)
(lambda (n)
(lambda (p)
(n m p)))))
(((f 5) +) (- 7 3))
ANS: 9
E. ( (lambda (y) (y 0)) (lambda (x) x) )
ANS: 0
F. (let ((x 3))
(let ((x 7)
(y (- x 1))) ; The expression (- x 1) is evaluated OUTSIDE
(* x y))) ; the inner let, and so sees the "x=3" binding
ANS: 14.
G. ( (lambda (x y) (+ x y)) 2 3 4 )
ANS: ERROR - wrong number of arguments (3) to the procedure (expects 2)
----------------------------------------------------------------------
PROBLEM 5 (7 points)
Complete the following sentences, which are based on points
emphasized in the lectures.
A. When Rational Math, Inc. wrote code that looked like:
(define (+rat x y)
(cons (+ (* (car x) (cdr y))
(* (car y) (cdr x)))
(* (cdr x) (cdr y))))
they were guilty of ___ABSTRACTION VIOLATION______________________.
B. The three key elements of any programming language (or good
engineering system) are:
1. _____PRIMITIVES______________________
2. Means of __COMBINATION_______________
3. Means of __ABSTRACTION_______________
C. The ____CLOSURE_________________ property enables us to nest
procedure calls arbitrarily deeply by having their return values be of
the same type as the arguments of those procedures.
----------------------------------------------------------------------
PROBLEM 6 (19 points)
In this problem, we are interested in a tree representation that
allows us to store values on internal nodes of the tree, as well as
have any number of children from each node of the tree. For
example, we might draw such a tree as:
30
/ \
/ \
5 6
/|\
/ | \
/ | \
3 2 1
/ \
/ \
1 2
The following data abstraction is used. A node is assumed to have
both a VALUE and a list of CHILDREN nodes. The predicate LEAF?
returns true if the node has no children (in which case it still has a
value, but the list of children is the empty list).
(define (make-node value children)
(list value children))
(define (node-value node)
(car node))
(define (node-children node)
(cadr node))
(define (leaf? tree)
(null? (node-children tree)))
The tree shown at the top of the page is generated using:
(define big-tree
(make-node
30
(list (make-node 5 nil)
(make-node 6 (list (make-node 3 nil)
(make-node 2 (list (make-node 1 nil)
(make-node 2 nil)))
(make-node 1 nil))))))
A. The following SMALL-TREE is generated:
(define small-tree
(make-node 10 (list (make-node 3 nil)
(make-node 4 nil))))
Draw a box-and-pointer diagram corresponding to SMALL-TREE.

B. We would sometimes like to see if a tree obeys a particular
consistency requirement. In particular, we would like to check if the
value of a node is equal to some operation on the values of the
children of that node. For example, we might want a node value to be
equal to the product of the values of its children. In the case of
BIG-TREE, it does satisfy this condition, while SMALL-TREE does not:
(check-tree * 1 big-tree) ==> #t
(check-tree * 1 small-tree) ==> #f
The following procedure is intended to perform this check. You are to
complete the procedure by providing the missing expressions.
(define (check-tree op init tree)
(define (check-subtrees children) ; children should be a LIST of nodes
(if (null? children)
#t
(and (check-tree op init ( children)) ; first child
(check-subtrees ( children))))) ; rest of children
(if (leaf? tree)
#t
(and (= ( tree)
(accumulate op init (map node-value (node-children tree))))
(check-subtrees (node-children tree)))))
= ANS: CAR
= ANS: CDR
= ANS: NODE-VALUE
PROBLEM 6, Continued
C. We next want a procedure that aggregates leaf information into node
information in a new tree. For example, we might like to copy the
BIG-TREE above, but instead of the node values being equivalent to the
product of the values of the children, we might want the node values
to be equal to the sum of the values of the children (throughout the
entire tree). If a node is a leaf node, we just copy the node value
for that leaf.
For example, we would like (TRANSFORM-TREE + 0 TEST-TREE) to produce
a new tree that looks like:
**
NOTE BUG: TEST-TREE above should be SMALL-TREE
**
12 (where the top node value 12 = 5+7)
/ \
/ \
5 7 (where the right node value 7 = 3+3+1)
/|\
/ | \
/ | \
3 3 1 (where the middle node value 3 = 1+2)
/ \
/ \
1 2
Complete the definition of the TRANSFORM-TREE procedure,
which looks very similar to the CHECK-TREE procedure with
only small changes. (The and you previously
wrote should still work here.)
(define (transform-tree op init tree)
(define (transform-subtrees children)
(if (null? children)
nil
( (transform-tree op init ( children))
(transform-subtrees ( children)))))
(if (leaf? tree)
(make-node (accumulate op init (map node-value
(node-children tree)))
(transform-subtrees (node-children tree)))))
** NOTE BUG: The (if ...) above should be
(let ((new-subtrees (transform-subtrees (node-chilren tree))))
(if (leaf? tree)
(make-node (accumulate op init (map node-value new-subtrees))
new-subtrees)))
**
= ANS: CONS
= ANS: TREE
----------------------------------------------------------------------
LIST HANDLING PROCEDURES
Definitions are provided here for your convenience.
(define (append s1 s2)
(if (null? s1)
s2
(cons (car s1)
(append (cdr s1) s2))))
(define (length lst)
(if (null? lst) 0 (+ 1 (length (cdr lst)))))
(define (map op lst)
(if (null? lst)
nil
(cons (op (car lst))
(map op (cdr lst)))))
(define (filter pred lst)
(cond ((null? lst) nil)
((pred (car lst))
(cons (car lst) (filter pred (cdr lst))))
(else (filter pred (cdr lst)))))
(define (accumulate op init lst)
(if (null? lst)
init
(op (car lst)
(accumulate op init (cdr lst)))))

