MASSACHVSETTS INSTITVTE OF TECHNOLOGY
Department of Electrical Engineering and Computer Science
6.001--Structure and Interpretation of Computer Programs
Fall Semester, 1998

Problem Set 5

Streams

• Issued: Thursday, October 15, 1998
• Tutorial preparation for: Week of October 19, 1998
• Written solutions due: Friday, October 23, 1998 before recitation
• Reading: Sections 3.1 and 3.3.1 for lecture on October 20, and Section 3.2 for lecture on October 22.

Part 1: Tutorial exercises

Prepare the following exercises for oral presentation in tutorial:

Tutorial exercise 1:

Do exercise 3.51 of the text which takes a closer look at delayed evaluation and stream-enumerate-interval.

Tutorial exercise 2:

Describe the streams produced by the following definitions. Assume that integers is the stream of non-negative integers (starting from 1):

 
(define A (cons-stream 1 (scale-stream 2 A)))

(define (mul-streams a b)
  (cons-stream
   (* (stream-car a) (stream-car b))
   (mul-streams (stream-cdr a)
                (stream-cdr b))))

(define B (cons-stream 1 (mul-streams B integers)))

Tutorial exercise 3:

Louis Reasoner wants to create an abstract constructor adjoin-term similar to that used for polynomials in the Generic Arithmetic System of Problem Set 4. He tries to define the following:

(define adjoin-term cons-stream)

but gets an error he doesn't understand. What is wrong?

He next tries the following:

(define (adjoin-term term series)
   (cons-stream term series)

Since this does not produce an error, he shows his definition to Alyssa P Hacker, who says, "Louis, you really don't understand the differences between special forms and procedures, do you?" What is she talking about? What would happen if Louis used his constructor in the following manner to define the series whose coefficients are all 1:

(define (one-series k)
  (adjoin-term (make-term k 1)
               (ones-series (+ k 1))))

and then attemped to evaluate (stream-car (ones-series 0))?

Tutorial exercise 4

Given a stream s the following procedure returns the stream of all pairs of elements from s:

(define (stream-pairs s)
  (if (stream-null? s)
      the-empty-stream
      (stream-append
       (stream-map
        (lambda (sn) (list (stream-car s) sn))
        (stream-cdr s))
       (stream-pairs (stream-cdr s)))))

(a) Suppose that integers is the (finite) stream {1, 2, 3, 4, 5}. What is (stream-pairs s)? (b) Give the clearest explanation that you can of how stream-pairs works. (c) Suppose that s is the stream of positive integers. What are the first few elements of (stream-pairs s)? Can you suggest a modification of stream-pairs that would be more appropriate in dealing with infinite streams?

Part 2: Laboratory--Working with Power Series

In lecture a few weeks ago, we saw how polynomials could be represented as lists of terms. In a similar way, we can represent power series, such as

$$\begin{eqnarray*}e^{x} &=& 1+x+\frac{x^{2}}{2}+\frac{x^{3}}{3\cdot2}+\frac{x^{4}... ...ac{x^{3}}{3\cdot 2}+\frac{x^{5}}{5\cdot 4\cdot 3\cdot 2}- \cdots \end{eqnarray*}$$

as streams of infinitely many terms. That is, the power series

$$\{ a_0 + a_1 x + a_2 x^2 + a_3 x^3 + \cdots \}$$

will be represented as the infinite stream whose elements are $\{a_0, a_1, a_2, a_3, \ldots\}$.¹

Implementing a Power Series as a Stream

We provide two ways to construct a series: coeffs->series and proc->series. The procedure coeffs->series takes a list of initial coefficients and pads it with zeroes to produce a powers series. For example, (coeff->series '(1 3 4)) produces the power series $1+3x+4x^2+0x^3+0x^4+\ldots{}$.

(define (coeffs->series list-of-coeffs)
  (define zeros (cons-stream 0 zeros))
  (define (iter lst)
    (if (null? lst)
        zeros
        (cons-stream (car lst)
                     (iter (cdr lst)))))
  (iter list-of-coeffs))

The other constructor, proc->series, takes as argument a procedure p of one numeric argument and returns the series

$$p(0) + p(1)x + p(2)x^2 + p(3)x^3 + \cdots$$

In the definition of proc->series, the stream non-neg-integers, which you will define in this problem set, is the stream of non-negative integers: { $0,1,2,3,\ldots{} \}$.

(define (proc->series proc)
  (stream-map proc non-neg-integers))

Other Stream Operations

With this representation, we can use basic stream operations such as:

(define (add-streams s1 s2)
  (cond ((stream-null? s1) s2)
        ((stream-null? s2) s1)
        (else
         (cons-stream (+ (stream-car s1) (stream-car s2))
                      (add-streams (stream-cdr s1)
                                   (stream-cdr s2))))))

(define (scale-stream c stream)
  (stream-map (lambda (x) (* x c)) stream))

to implement series operations, and thus arrive at a complete power series data abstraction:

(define add-series add-streams)

(define scale-series scale-stream)

(define (negate-series s)
  (scale-series -1 s))

(define (subtract-series s1 s2)
  (add-series s1 (negate-series s2)))

(define (show-series s nterms)
  (if (= nterms 0)
      'done
      (begin (write-line (stream-car s))
             (show-series (stream-cdr s) (- nterms 1)))))


{\small \begin{verbatim}
(define (series-coeff s n)
  (stream-ref s n))

You will find the show-series procedure helpful because it allows you to examine the series that you will generate in this problem set. You can also examine an individual coefficient (of xⁿ) in a series using series-coeff.

Note: Loading the code for this problem set will change Scheme's basic arithmetic operations +, -, *, and / so that they will work with rational numbers. For instance, (/ 3 4) will produce 3/4 rather than .75. You'll find this useful in doing the exercises below.

Lab exercise 1:

Load the code for problem set 5 (file ps5-code.scm). Define the stream non-neg-integers. Show how to define the series:

$$\begin{eqnarray*}S_1 &=& 1 + x + x^2 + x^3 + \cdots \cr S_2 &=& 1 + 2x + 3x^2 + 4x^3 + \cdots \end{eqnarray*}$$

Turn in your definitions and a couple of coefficient printouts to demonstrate that they work.

Lab exercise 2:

Complete the definition of the following procedure, which multiplies two series:

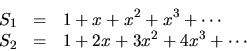
(define (mul-series s1 s2)
  (cons-stream < ??E1?? >
               (add-series < ??E2?? >
                           < ??E3?? > )))

To test your procedure, demonstrate the the product of S₁ (from exercise 1) and S₁ is S₂. What is the coefficient of x¹⁰ in the product of S₂ and S₂? Turn in your definition of mul-series. (Optional: Give a general formula for the coefficient of xⁿ in the product of S₂ and S₂.)

Inverting a power series

Let S be a power series whose constant term is 1. We'll call such a power series a ``unit power series.'' Suppose we want to find the inverse of S, 1/S, which is the power series X such that $S\cdot X= 1$. Write S=1+S_R where S_R is the rest of S after the constant term. Then we can solve for X as follows:

$$\begin{eqnarray*}S \cdot X &=& 1 \cr (1+S_R)\cdot X &=& 1 \cr X + S_R \cdot X &=& 1 \cr X &=& 1 - S_R \cdot X \end{eqnarray*}$$

In other words, X is the power series whose constant term is 1 and whose rest is given by the negative of S_R times X.

Lab exercise 3:

Use this idea to write a procedure invert-unit-series that computes 1/S for a unit power series S. You will need to use mul-series. To test your procedure, invert the series S₁ (from exercise 1) and show that you get the series 1-x. (Convince yourself that this is the correct answer.) Turn in a listing of your procedure. This is a very short procedure, but it is very clever. In fact, to someone looking at it for the first time, it may seem that it can't work--that it must go into an infinite loop. Write a few sentences of explanation explaining why the procedure does in fact work, and does not go into a loop.

Lab exercise 4:

Write a procedure div-series that divides two power series. Div-series should work for any two series, provided that the denominator series begins with a non-zero constant term. (If the denominator has a zero constant term, then div-series should signal an error.) You may find it useful to reuse some answer from a previous exercise in this problem set. Turn in a listing of your procedure along with three or four well-chosen test cases (and demonstrate why the answers given by your division are indeed the correct answers).

Lab exercise 5:

Define a procedure integrate-series-tail that, given a series

$$a_0 + a_1 x + a_2 x^2 + a_3 x^3 + \cdots$$

returns the integral of the series (except for the constant term)

$$a_0 x + \frac{1}{2}a_1 x^2 + \frac{1}{3}a_2 x^3 + \frac{1}{4}a_3 x^4 + \cdots$$

Turn in a listing of your procedure and demonstrate that it works by computing integrate-series-tail of the series S₂ from exercise 1.

Lab exercise 6:

Demonstrate that you can generate the series for e^x as

(define exp-series
  (cons-stream 1 (integrate-series-tail exp-series)))

Explain the reasoning behind this definition. Show how to generate the series for sine and cosine, in a similar way, as a pair of mutually recursive definitions.

Lab exercise 7:

Louis Reasoner is unhappy with the idea of using integrate-series-tail separately. ``After all,'' he says, ``if we know what the constant term of the integral is supposed to be, we should just be able to incorporate that into a procedure.'' Louis consequently writes the following procedure, using integrate-series-tail:

(define (integrate-series series constant-term)
  (cons-stream constant-term (integrate-series-tail series)))

He would prefer to define the exponential series as

(define exp-series
  (integrate-series exp-series 1))

Write a two or three sentence clear explanation of why this won't work, while the definition in exercise 6 does work.

Lab exercise 8:

Write a procedure that produces the derivative of a power series. Turn in a definition of your procedure and some examples demonstrating that it works.

Lab exercise 9:

Generate the power series for tangent, cotangent, and secant. List the first ten or so coefficients of each series. Demonstrate that the derivative of the tangent is the square of the secant.

Lab exercise 10:

The Bernoulli numbers B_n are defined by the coefficients in the following power series: ²

$$\frac{x}{e^x-1} = B_0 + B_1 x + \frac{B_2 x^2}{2!} + \frac{B_3 x^3}{3!} + \cdots = \sum_{k \geq 0} \frac{B_k x^k}{k!}$$

Write a procedure that takes n as an argument and produces the nth Bernoulli number. (Check: All the odd Bernoulli numbers are zero except for B₁=-1/2.) Generate a table of the first 10 (non-zero) Bernoulli numbers. Note: Since e^x-1 has a zero constant term, you can't just use div-series to divide x by this directly.

Lab exercise 10:

It turns out that the coefficient of x^2n-1 in the series expansion of $\tan x$ is given by

$$\frac{(-1)^{n-1} 2^{2n} (2^{2n} - 1) B_{2n}}{(2n)!}$$

Use your series expansion of tangent to verify this for a few of values of n.

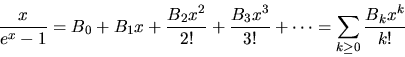
Turn in answers to the following questions along with your answers to the questions in the problem set:

1.

About how much time did you spend on this homework assignment? (Reading and preparing the assignment plus computer work.)

2.

Which scheme system(s) did you use to do this assignment (for example: 6.001 lab, your own NT machine, your own Win95 machine, your own Linux machine)?

3.

We encourage you to work with others on problem sets as long as you acknowledge it (see the 6.001 General Information handout).

• If you cooperated with other students, LA's, or others, or found portions of your answers for this problem set in references other than the text (such as some of the archives), please indicate your consultants' names and your references. Also, explicitly label all text and code you are submitting which is the same as that being submitted by one of your collaborators.
• Otherwise, write ``I worked alone using only the reference materials,'' and sign your statement.

About this document ...

This document was generated using the LaTeX2HTML translator Version 98.1p1 release (March 2nd, 1998)

Copyright © 1993, 1994, 1995, 1996, 1997, Nikos Drakos, Computer Based Learning Unit, University of Leeds.

The command line arguments were:
latex2html ps5-series.

The translation was initiated by Tony Eng on 1998-10-16