Meeting 2: Geometry, Graphics, Interaction Preliminaries

Presenters: Neel, Prof. T

Resources:

• Blinn Chapter 8, "Where Am I? What Am I Looking At?"
• Blinn Chapter 18, "The Homogeneous Perspective Transform"
• Demos in 6.838 locker
• xforms
• SGI OpenGL

• Geometric primitives, operators
• Coding infrastructure for exercises (gvis)
• Exercise 1
• Student presentations -- scheduling

Computational Constructions in 3D

  Primitives:

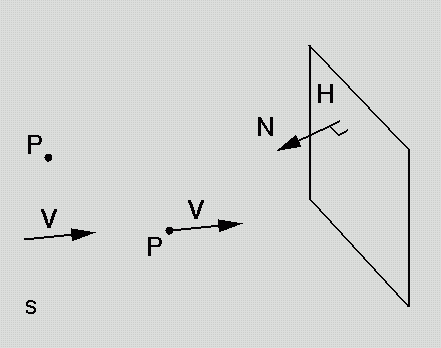
  Scalar    s = <x>

      Point     P = <x, y, z>

  Vector    V = <x, y, z>

  Plane     H = <A, B, C, D> = <N, D>
    H(P) = N^.P + D = scalar function
    Plane is zero set of this function.
        [Note halfspaces H⁺, H^-.]
    What is plane normal?  Why?
 
  Ray       R = <P, V>
    I.e., a point and a direction

  Operators/Constructors:

 [Conventions ?  Failure cases ?]

    Length (L2 norm) of vector V:
  L(V)= |V| = sqrt(V.x^2 + V.y^2 + V.z^2)
  (Note C-like "." operator for accessor)

     Vector V from P to Q:   V = Q - P

  Unit vector V' = V/L(V) = Unit(V)

    Plane H normal to unit vector
    N, containing point P

    H.N = N
            H.D = ?

     Arithmetic argument:
    H(P) = 0 = N^.P + D
    D by inspection.
 

 
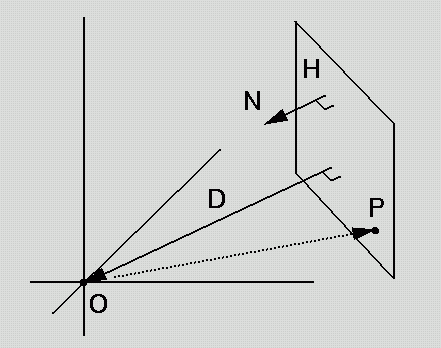
  Geometric argument:
    Interpret P as vector from origin
    Express altitude D in terms of P, N
        (what is known about D, N ?)
    D = -N(N^.P), D = -|D| by inspection.

  Summary of Plane constructors:
    [Conventions ?  Failure cases ?]
    Four scalars
    (Unit) Vector, scalar
    Vector, point
    Three points
    Two vectors, one point
    Two points, one vector
        [two interpretations]

Notation:

  Inner product ^. : N^.P     (scalar)

  Cross product x : N x P     (vector)

  Flat (concatenation): PQ  (subspace)

  Intersection ^ :  PQ ^ H  (subspace)
 

Operators:

0) Signed distance of P from plane <N,D>

  H^.P = N^.P + D  [note abusive notation]

1) Intersect ray <R,V> with plane <N,D>

  Ray is parametric:  P(t) = R + t V
 
  Plane is implicit:  H^.P(t) = 0

  Solve for t which satisfies both:

    H^.P(t) = (N^.R + t N^.V) + D = 0

    t = -(N^.R + D)/N^.V

    What is intersection point ?

2) Intersect ray <R,V> with sphere <C,r>

  Ray is parametric:  P(t) = R + tV

  Sphere is implicit: (P-C)^.(P-C) = r²

  Solve for t which satisfies both:

    (R + tV - C)^.(R + tV - C) = r²

    t = ...

3) Nearest pt P on sphere to given ray?

 There is a closed form solution.  But...
 
 there is also a much easier way - what?

 Find point P "by construction"!

 0) Given ray <R,V>; sphere <C,r>

 1) Construct plane H from V, C

 2) Intersect <R,V> with H to find L
 
 3) Intersect CL with sphere to find P

    Express in closed form as:

        P = C + D UnitVector(C, L)

 4) What is the nearest point on ray ?
 

4) Line-line (ray-ray) closest approach:

 (Closed-form: parametrize in s,t;
  minimize w.r.t. both parameters)
 

 0) Given ray <P,Q>; ray <R,S>

 1) Form A = Q x S

 2) H_PQA = Plane(P, Q, A)

 3) H_RSA = Plane(R, S, A)

 4) B (on PQ) is PQ ^ H_RSA

 5) C (on RS) is RS ^ H_PQA

_{And many others.  But how to use them?
Examples, introduction to gvis.}
 

Meeting 3 (Wednesday): Primitives, Duality [Marc]

Previous Meeting .... Next Meeting ... Course Page

Last modified: Feb 1998