The Road to Duality

Presentation by: Marc Lebovitz

---

My friend and yours: Cartesian Coordinate System (2D)

• Point vs. Vector
both can be represented by 2 floats in 2D
distinguish between the two by an extra bit
• Line thru 2 Points
For now, let's represent the line in slope/intercept form: y=mx+b
points (a,b) and (c,d) => line y = (b-d/a-c)x + b - (a(b-d)/a-c)
when undefined: a=c ... when the line is vertical

• Leftof
Let's find how far a point lies from a line and on which side.
We can now try the new line representation: Ax+By+C=0.
A,B give the normal vector to the line and C is the offset.
To find the distance, plug x and y into the line equation Ax+By+C.
But be careful!  The correct distance is given only if A,B are normalized.
If the resulting distance is positive, the point lies in the direction of the line's normal.
Note: A line can be represented with its normal pointing in either direction.
Ex.: line y=2x --> 2x-y+0=0.  Point (1,-1)
       2(1) + (-1)(-1) + 0  =  3
       Since we didn't normalize the line, 3 is not the actual distance to the point.
       However, since our calculations gave a positive number, the point lies in the direction of
            the normal from the line.  In this case it is on the right and below the line.
What is this new representation, Ax+By+C=0 good for?  It allows vertical lines!

• Point of Intersection of 2 Lines
Now that we have taken care of vertical lines in Cartesian coordinates, we run into another problem: points at infinity.
Let's find the intersection of 2 lines:
    Lines: Ax+By+C=0 and Dx+Ey+F=0 ... find their intersection by solving for x,y.
Ex. 1: x-y+0=0 and x+0y-2=0    intersect at (2,2)
Ex. 2: x+0y-2=0 and x+0y-1=0    intersect at....???? we don't know!
when undefined: when lines are parallel, point of intersection is at infinity

---

Our new best friend: Homogeneous Coordinate System

• Intro
The major drawback of the Cartesian coordinate system is that it fails to represent points at infinity. To gain a grasp of the Homogeneous space, think of taking a point x,y and moving along the vector in that direction toward infinity. The line along which we have just travelled is the homogeneous representation of our point. At infinity, picture the x and y of the point as being divided by 0. This point at infinity now has a direction, the numerator of x and y. If we divided them by 1 instead, we return to our original point. To divide by any other number will yield a different point on the line we have just defined. Let's take this denomenator and make it a third parameter, extending our 2D Cartesian space to a 3D Homogeneous space. We'll call the new parameter w. The point (x,y) now becomes the line (x,y,w).

• Conversion to Cartesian Space...(x,y,w) => (x,y)
• Mathematical: Divide x and y by w to yield the (x,y) point in Cartesian space.
• Intuitive: The Cartesian space consists of all points on all lines in the Homogeneous space with w=1. This is the plane at w=1. When your homogeneous point has a w other than one, simply project that point onto the Cartesian plane at w=1.

• Point-Line Relations
Now that points and lines both are represented by three floats: (x,y,w) and (A,B,C) (from Ax+By+C=0)
we can do interesting stuff:
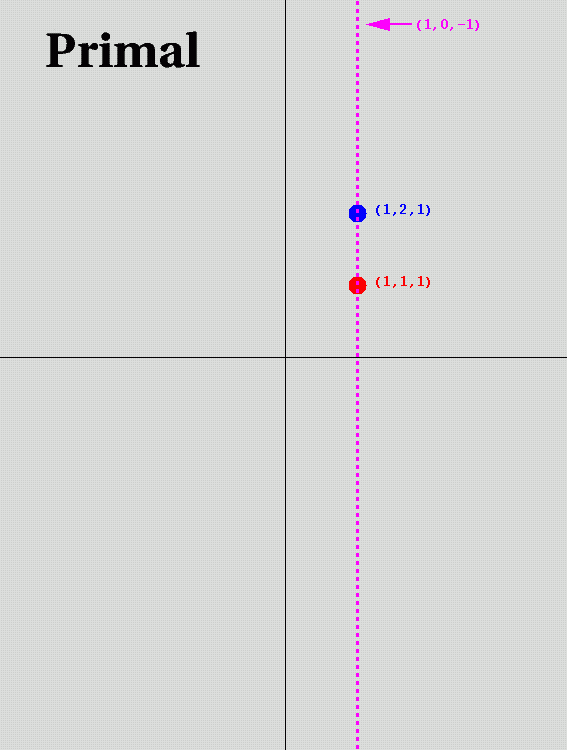
• Point-Line Incidence: P ^. L = 0
Ex: Point (2,2) and line (1,0,-2) ... P ^. L = 0!
      Note how easily vertical lines are handled.
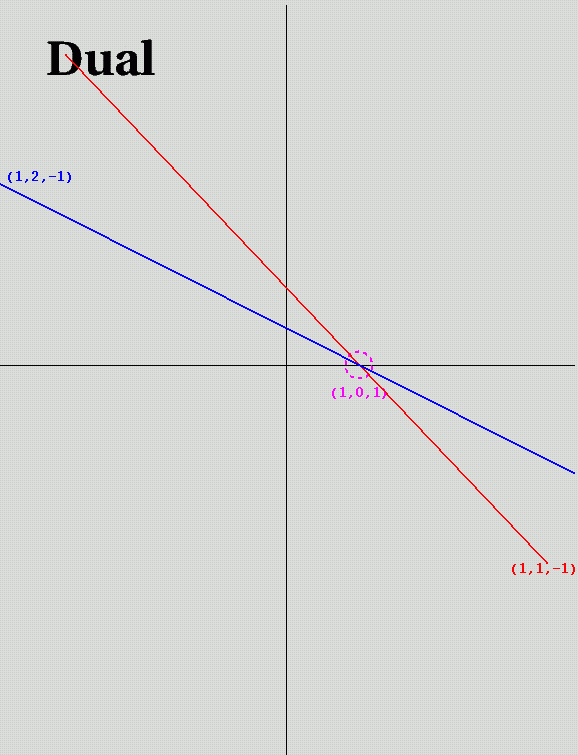
• Line thru 2 Points: L = P1 x P2
Ex: Point (2,2) and Point (2,1) ... yield line (1,0,-2)
      Again, vertical lines aren't a problem.
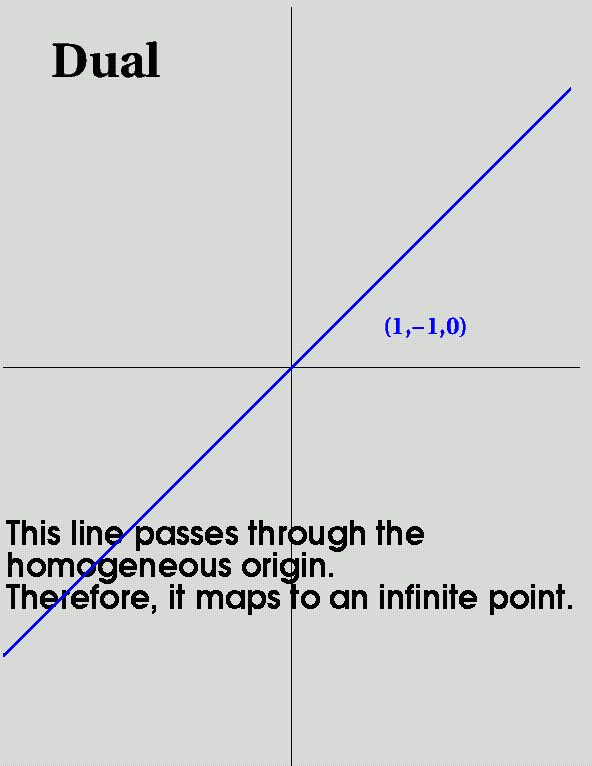
• Point of Intersection of 2 Lines: P= L1 x L2
Ex: Line (1,0,-1) and line (1,0,-2) ... yield point (0,1,0)
      This makes sense...the point at infinity in the direction (0,1)
      Now we have handled infinite points!

• What's not defined
There is a point which is not defined in Homogeneous space, the origin. In 2D Homogeneous space, this is the point (0,0,0).
It cannot exist because its inner dot product with all lines = 0. This means that it is on all lines in the Homogeneous space.
That, in turn, means that all points in Cartesian space are incident with one line. Clearly, this is not possible.

---

Introducing....Duality!

• 2 Representations of a Line
The line, Ax+By+C=0 can also be written as a point (A,B,C).
The line L becomes the point L*.
Similarly, the point P can be written as a line P*.
Normal representations are viewed in the "Primal" plane.
Alternate representations are viewed in the "Dual" plane.

• Collineation
A transform which takes lines to lines.  It has the consequence that incidence is preserved.
P ^. L = P^{* .} L^*= 0.

• Duality
The existence of this mapping implies that every theorem, definition, or algorithm has a dual definition
by simply exchanging the word point with the word line.
Ex.: There exists a unique line incident to any 2 points. => There exists a unique point incident to any 2 lines.
Homogeneous representation is necessary here because degeneracies would create special cases that
would prevent easy mapping of the theorems, algorithms, and definitions.
More complex dualities to come!
Consider the line representation:     A=x, B=y, C=-w
Note that incidence is preserved.
     
What happens in degenerate cases?

 

---

In This Corner: Classical vs. Oriented Projective Geometry

• Classical Projective Geometry Drawbacks
The classical projective geometry we have been using here has drawbacks. Consider the line (x,y,w) in
Homogeneous space. The point at (x,y,1) can move along the line in two directions toward infinity. That
means that points in opposite directions along the line correspond to the same point at infinity.
Visually, the plane is a twisted torus.
What does this mean to us?
• Non-Orientable Plane
We can continuously transport a left turn over the plane so that it returns with its sense reversed. Therefore, clockwise is not defined.
• 1-Sided Lines
If you cut a plane along a straight line, you are left with a disk.
• Segments are Ambiguous
2 arcs exist between any two points...the one that passes through infinity and the one that doesn't.

• Directions are Ambiguous
• No such thing as convex figures

• Oriented Projective Geometry
Each classical line is replaced by 2 lines with opposite orientations: (x,y,w) , (-x,-y,-w)
=> Double covering of plane. (circular orientation)
The projective plane is now 2-sided.
Dualities now preserve not only incidence, but also orientation!

---

Duality and You: A case study.

• Using Idual
Draw:    pick point/line/circle
                leftclick to add a point (lines and circles require 2 points to define)
                rightclick your point when adding your last item to your data object
                        for lines, circles, leftclick point 1 and rightclick point 2 for last one
                for precise coordinates, hold down "Ctrl" key and enter them into dialogue box
                also, snapping is possible with 'N'....undo with 'Shift N'
Undo:    undo/redo->remove/restore most recently added object
                undo/redo all -> remove/restore all objects
                clear all -> remove all objects with no hope of redoing
                clear undo -> clear the undo buffer
"Cycle" button:    to conserve space, multiple menus can be reached by this button
                                1st menu: colormap, add window, environment buttons
                                2nd menu: load/merge objects and save drawing to file/standard output
                                3rd menu: add/edit/delete/undelete dualities
Colors:    autocolor chooses colors at random
                leftclick on "choice button" to cycle through color schemes
                rightclick on "choice button" to see all possible color schemes
                manual colors are possible...choose that scheme and press "Colormap" button for color choice
Window view:    zoom in with shift keys and left mousebutton
                             zoom out with shift keys and right mousebutton
                              'C' key changes state window 'center'
                              'V' key toggles Fixed/Dynamic Views:
                                      Fixed View window: translation locked
                                      Dynamic View window: translation possible
                              'space': change window duality
Horizontal Control Panel:        change line/wedge representations
Viewing Multiple Dualities:    set duality to Omega...draw in Primal and all duals will appear in Dual
                                                     to view a subset of the dualities, 'delete' undesirable dualities
                                                            note: this is NOT permanent...'undelete' it to bring it back
 
• Things to know about dualities
Line Segment -maps to-> double wedge
        why: endpoints map to 2 intersection lines
                  points between them map to lines within the double wedge
        how: extend segment to line....any point on the line will map to a line incident with the point which
                  is dual to the line.  Therefore, intersection of 2 endpoint lines is dual of line extended from
                  segment.  Therefore, any point on the segment will map to a line which hits this endpoint.
        which double wedge determined by the two endpoints?: unsolvable problem in general

• New Dualities

Duality	Dual of (a,b)	Dual of y=ax+b	Dual of ax+by+1 = 0
Brown	y=ax+b	(-a,b)	(a/b , -1/b)
Stolfi	ax+by+1=0	(a/b , -1/b)	(a,b)
Edelsbrunner	y=2ax-b	(a/2 , -b)	(a/-2b , 1/b)
Inversion	( a/(a2+b2) , b/(a2+b2) )	(x +a /2b)2 + (y - 1/2b)2 = a2+1 / 4b2	(x + a/2)2 + (y - 1/2)2 = a2+b2 / 4

 

• Example Applications
• Eliminating redundant halfspaces = Finding the convex hull of points
• Finding a line that intersects all line segments = Finding the intersection of all double wedges
• Finding the intersection of a set of circles whose boundaries contain the origin = Finding the intersection of a set of halfplanes