kD Trees
Nice features:
-
Search for points in a rectangular window in O( sqrt( n )
+ k )
-
Still O( n ) storage and O( n log n ) construction time
Description:
A tree. Each node an axis parallel split, with points in
leaves. 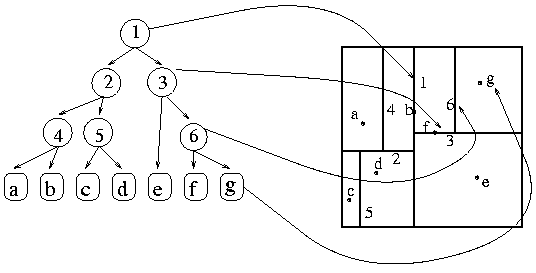
Construction:
For a Kd tree storing the two dimensional location of a set
of points:
Top Down:
P a set of points, depth the current depth
in the tree
BuildKdTree(P,depth)
if P contains only
one point
then return a leaf storing
the point
else if depth
is even
then
Split P into two subsets with a vertical
line l through the median x-coordinate of the points in
P. Let A be the set of points to the left
of l or on l, and B
be the set of points to the right of l.
else
Split P into two subsets with a horizontal
line l through the median
y-cooridnate of the points in P. Let A
be the set of points below l
or on l, and B be the set of points
above l.
Create a node v storing l
with children left and right
left <- BuildKdTree( A,
depth + 1 )
right <- BuildKdTree( B,
depth + 1 )
return v
It is expensive to find the meadian for each node; better
to create a list of sorted points for each dimension. Then it is pretty
easy to find the median quickly.
This procedure obviously generalizes to any dimension
of input.
Use:
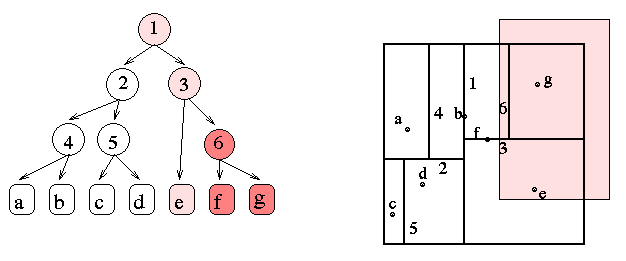
Finding the set of points within a window: if a node is completely
contained in a region, then all of its children also are.
v a node, R a range
SearchKdTree( v, R
)
if v is a leaf
then Report the point stored at v
if it lies in R
else
if region( v->left
) is fully contained in R
then ReportSubtree( v->left
)
else
if region( v->left
) intersects R
then SearchKdTree( v->left,
R )
if region( v->right )
is fully contained in R
then ReportSubtree( v->right
)
else
if region( v->right
) intersects R
then SearchKdTree( v->right,
R )
This structure is useful for arbitrary objects; let each
region in the graph be a bounding box for an object.
Find Nearest Neighbor to an object, O:
To find the nearest neighbor of a need to check all of
the objects in regions which intersect a box slightly larger than the region
containing O.
Or, walk the tree.
n-body problem
How can we efficiently simulate the movements of a collection
of objects moving under mutual gravational attraction?
Naive:
For each object, sum the force due to every other object.
Uses O( n2 ) time.
Multipole Expansion:
Compute from the bottom up; that is, for each subdivision
of space, figure out its total effect on the rest of space. Pass this quantity
on to the parent of the subdivision.
Put the objects into a tree.
Start at the bottom level of the tree,
For every region at a depth d in the tree:
If any children are leaves,
then compute the interaction directly
Compute the "Multipole Expansion"
Convert this into a local expansion for the parent
node and pass it up.
Move on to level d-1.
When we reach the top of the tree, recurse back down
the tree, summing the local expansions.
We are doing a calcultion on each node in the tree twice.
O( n ) nodes, so this is algorithm uses O( n ) time.
What happens to the data structure when points move around?

Color Reduction:
What is an intelligent way to take a pick 256 colors to represent
a full color image?
Naieve:
-
Pick the colors which are used most often. (want to reduce
the color space before trying this, so similar colors are not picked redundantly)
-
Find an exact solution (the 256 colors which maximize a fitness
function)
Median Cut Algorithm:
Build a tree with the set of colors used:
At each node, find the dimension with the largest
range.
Divide the set of colors on the median of that range.
Pass left half of the set to left child, right half
to right child.
Stop when there are the appropriate number of leaf
nodes.
For each leaf, average the colors contained by the
leaf.
Use these averages for the reduced palette.
[Start] [Back]
[Next]
Douglas De Couto
decouto@graphics.lcs.mit.edu
Joshua Napoli
napoli@mit.edu
Last modified: Tue Mar 17 09:49:02 1998


