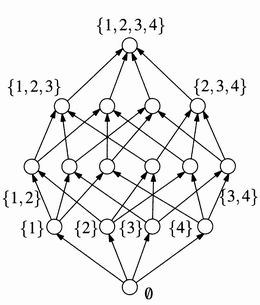
![]() The nodes
are all the subsets of S
The nodes
are all the subsets of S
![]() Arcs go
from every subset of size i to every subset of size i+1 containing it.
Arcs go
from every subset of size i to every subset of size i+1 containing it.
![]() Note that
directed paths from the empty set to S correspond to permutations
Note that
directed paths from the empty set to S correspond to permutations
6.838, Computational Geometry; Fall 2001
Point Location
Sergi Elizalde & David Pritchard
We have seen that the expected query time is good. However, for some points the query time can be bad.
We will see that the probability that this happens is small.
Lemma.
Let l>0 be a parameter. The probability that the search path for q has more than 3lln(n+1) nodes is at most 1/(n+1)l ln1.25-1
Proof
Consider the following acyclic graph:
 |
|
|
|
|
|
|
|
![]() Mark an arc if
the insertion of the corresponding element changes the trapezoid containing
q.
Mark an arc if
the insertion of the corresponding element changes the trapezoid containing
q.
![]() Using backwards
analysis, every node has at most 4 marked incoming arcs.
Using backwards
analysis, every node has at most 4 marked incoming arcs.
![]() Mark arbitrary
nodes so that every node has exactly 4 marked incoming arcs (with the exception
of those having less than 4 incoming arcs, for which we mark all of them).
Mark arbitrary
nodes so that every node has exactly 4 marked incoming arcs (with the exception
of those having less than 4 incoming arcs, for which we mark all of them).