6.838, Computational Geometry; Fall 2001

Point Location

Sergi Elizalde & David Pritchard

The Trapezoidal Map

Although the previous algorithm was inefficient in terms of space usage, it had some very nice properties:

- the entire map was broken into trapezoidal sections (and triangles, which we treat as degenerate trapezoids)

- each trapezoid has exactly 2 non-vertical boundaries

- no trapezoid contains a vertex (all are at corners)

- each trapezoid belongs to exactly one face

We want to preserve these properties but reduce the complexity of our structure

We can remove many edges without destroying these properties:

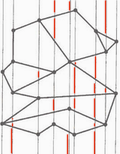
Removing all unnecessary edges gives us the trapezoidal map (also trapezoidal/vertical decomposition) T(S) of S

Formally, the trapezoidal map of S is obtained from S by taking a planar subdivision, and drawing two vertical extensions from each vertex: an upper vertical extension, and a lower vertical extension.

The extensions go vertically up/down from the vertices of S and stop when they hit an edge or the bounding box

The trapezoidal map is guaranteed to be not much more complex than the original map; if we started with n line segments than we can end up with no more than 3n+1 trapezoids (Lemma 6.2)