Computing closet point

• We can simplify the mesh (see the next talk)
• For a triangular mesh:
• First, we find the closest vertex in other mesh using 3D-trees as follows:
• Node v has two items:
• P(v): point through which the space is cut into two
• t(v) : taking values 0, 1 and 2, indicating the cutting plane is parallel to yz-, xz-, or xy-plane 

• The worst-case search time is in O(n^(2/3)), but when D_max is small, it  is faster, e.g.  O(logn)

 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 


 

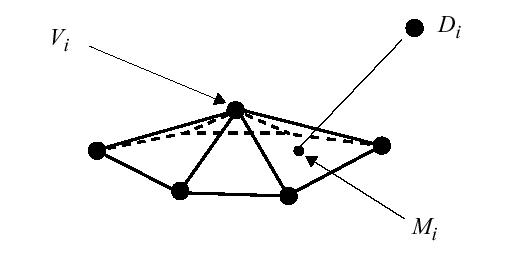
• For a triangular mesh:
•  Then, we find the closet point in a triangle which is the neighbor of  the vertex