Interpolating Parameters Over a Triangle's Area

Next we add a new capability to our triangle rasterizer; the ability to linearly interpolate parameters over its interior. You might ask: Why would we ever want to do such a thing? The reasons are plenty.

Currently we can only draw solid colored triangles. Wouldn't it be nice if we could smoothly vary the colors as we filled the polygon. In this case the parameters that are interpolated are the red, green, and blue components of the color. Later on, when we get to 3D techniques, we'll also interpolate other parameters such as the depth at each point on the triangle.

First, let's frame the problem. At each vertex of a triangle we have a parameter, say its redness. When we actually draw the vertex, the specified shade of red is exactly what we want, but at other points we'd like some sort of smooth transition between the values given. This situation is depicted below:

Notice that the shape of our desired redness function is planar. Actually, it is a special class of plane where there exists a corresponding point for every x-y coordinate. Planes of this type can always be expressed in the following form:

Where in our case the z-coordinate represents the redness of the vertex. This equation should appear familiar. It has the same form as our edge equations.

So, given three vertices each with its own redness, we can set up the following linear system.

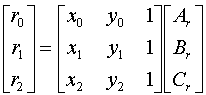
with the solution:

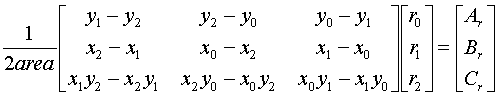
By the way, we've already computed these matrix entries, they're exactly the coefficients of our edge equations.

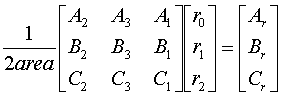
So the all the additional work that we need to do to interpolate is a single matrix multiplication and the equivalent of an extra edge equation for each additional parameter.

The following smooth triangle object implements these ideas. It begins with the typical constructor.

import Raster;
import Drawable;
import Vertex2D;
import FlatTri;

public class SmoothTri extends FlatTri implements Drawable {
    boolean isFlat;
    double scale;
    
    public SmoothTri(Vertex2D v0, Vertex2D v1, Vertex2D v2)
    {
        v = new Vertex2D[3];
        v[0] = v0;
        v[1] = v1;
        v[2] = v2;
        
        /*
            check if all vertices are the same color
        */
        isFlat = (v0.argb == v1.argb) && (v0.argb == v2.argb);
        if (isFlat) {
            color = v0.argb;
        } else {
            color = 0;
        }
        
        /*
            Scale is always non zero and positive. This zero
            value indicates that it has not been computed yet
        */
        scale = -1;
    }

I've added two new instance variables. The first is simply an optimization that detects the case when all three vertices are the same color. In this case we'll call the slightly faster FlatTri methods that we inherited.

    public void PlaneEqn(int eqn[], int p0, int p1, int p2)
    {
        int Ap, Bp, Cp;
        if (scale <= 0) {
            scale = (1 << EdgeEqn.FRACBITS) / ((double) area);
        }
        double sp0 = scale * p0;
        double sp1 = scale * p1;
        double sp2 = scale * p2;
        Ap = (int)(edge[0].A*sp2 + edge[1].A*sp0 + edge[2].A*sp1);
        Bp = (int)(edge[0].B*sp2 + edge[1].B*sp0 + edge[2].B*sp1);
        Cp = (int)(edge[0].C*sp2 + edge[1].C*sp0 + edge[2].C*sp1);
        eqn[0] = Ap;
        eqn[1] = Bp;
        eqn[2] = Ap*xMin + Bp*yMin + Cp + (1 << (EdgeEqn.FRACBITS - 1));
    }

    public void Draw(Raster raster)
    {
        if (isFlat) {
            super.Draw(raster);
            return;
        }
        
        if (!triangleSetup(raster)) return;
        int alpha[] = new int[3];
        int red[] = new int[3];
        int green[] = new int[3];
        int blue[] = new int[3];
        
        int t0 = v[0].argb;
        int t1 = v[1].argb;
        int t2 = v[2].argb;
        PlaneEqn(blue, t0 & 255, t1 & 255, t2 & 255);
        t0 >>= 8;   t1 >>= 8;   t2 >>= 8;
        PlaneEqn(green, t0 & 255, t1 & 255, t2 & 255);
        t0 >>= 8;   t1 >>= 8;   t2 >>= 8;
        PlaneEqn(red, t0 & 255, t1 & 255, t2 & 255);
        t0 >>= 8;   t1 >>= 8;   t2 >>= 8;
        PlaneEqn(alpha, t0 & 255, t1 & 255, t2 & 255);
        
        int x, y;
        int A0 = edge[0].A; int A1 = edge[1].A; int A2 = edge[2].A;
        int Aa = alpha[0];
        int Ar = red[0];    int Ag = green[0];  int Ab = blue[0];
        
        int B0 = edge[0].B; int B1 = edge[1].B; int B2 = edge[2].B;
        int Ba = alpha[1];
        int Br = red[1];    int Bg = green[1];  int Bb = blue[1];
        
        t0 = A0*xMin + B0*yMin + edge[0].C;
        t1 = A1*xMin + B1*yMin + edge[1].C;
        t2 = A2*xMin + B2*yMin + edge[2].C;
        int ta = alpha[2];
        int tr = red[2];    int tg = green[2];  int tb = blue[2];
        
        yMin *= raster.width;
        yMax *= raster.width;

        /*
             .... scan convert triangle ....
        */
        for (y = yMin; y <= yMax; y += raster.width) {
	        int e0 = t0;    int e1 = t1;    int e2 = t2;    int xflag = 0;
	        int a = ta;     int r = tr;     int g = tg;     int b = tb;
	        for (x = xMin; x <= xMax; x++) {
	            if ((e0|e1|e2) >= 0) {      // all 3 edges must be >= 0
	            	int pixa = (a >> EdgeEqn.FRACBITS);
                    int pixr = (r >> EdgeEqn.FRACBITS);
	                int pixg = (g >> EdgeEqn.FRACBITS);
	                int pixb = (b >> EdgeEqn.FRACBITS);
                    pixa = ((pixa & ~255) == 0) ? pixa << 24 : ((a < 0)	? 0 : 0xff000000);
                    pixr = ((pixr & ~255) == 0) ? pixr << 16 : ((r < 0)	? 0 : 0x00ff0000);
                    pixg = ((pixg & ~255) == 0) ? pixg << 8  : ((g < 0)	? 0 : 0x0000ff00);
                    pixb = ((pixb & ~255) == 0) ? pixb       : ((b < 0)	? 0 : 0x000000ff);
		            raster.pixel[y+x] = (pixa | pixr | pixg | pixb);
		            xflag++;	            
	            } else if (xflag != 0) break;
	            e0 += A0;   e1 += A1;   e2 += A2;
	            a += Aa;    r += Ar;    g += Ag;    b += Ab;
	        }
	        t0 += B0;   t1 += B1;   t2 += B2;
	        ta += Ba;   tr += Br;   tg += Bg;   tb += Bb;
        }
    }
}

Return to index