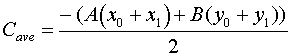Numerical Percision of the C Coefficient
Computers represent floating-point number internally in a format similar
to scientific notation. The very worse thing that you can do with numbers represented
in scientific notation is subtract numbers of similar magnitude. Here is what happens:
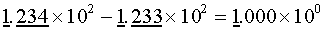
We loose most of the significant digits in our result.
In the case of triangles, these sort of precision
problems to occur frequently, because in general the vertices
of a triangle are close to each other.
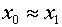 and and
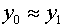 thus thus
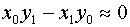
Thankfully, we can avoid this subtraction of large numbers when
computing an expression for C. Given that we know A and
B we can solve for C as follows:
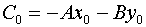 or
or 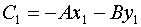
To eliminate any bias toward either vertex we will average of these C values
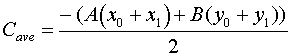
|
 |
Lecture 7 |
|
Slide 13 |
|
6.837 Fall '98 |
 |
In order to understand the expression for C that we'll
use it is necessary to discuss the numerical precision of the floating point
calculations used by computers. Computers represent floating-point
number internally in a format similar to scientific notation.
Each number is stored with fractional part having a fixed number
of significant digits along with an exponent. If you remember
back to you chemistry or physics classes, the very worse thing
that you can do with numbers represented in scientific notation
is subtract numbers of similar magnitude. Here is what happens.
Suppose we have four significant digits in our notation. If we
subtract numbers of similar magnitudes as shown below:
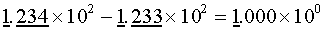
We loose most of the significant digits in our result.
In the case of triangles, we can expect these sort of precision
problems to occur frequently, because in general the vertices
of a triangle are usually relatively close to each other.
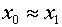 and
and
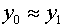 thus
thus
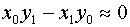
Thankfully, we can avoid this subtraction of large numbers when
computing an expression for C. Given that we know A and
B we can solve for C as follows:
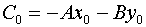 or
or 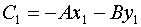
In order to eliminate any unnecessary bias toward either vertex
in our calculation we can compute the average of these C values
as follows.
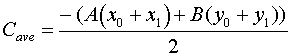
This is the expression for C that we'll use in our method,
and it avoids many of the numerical problems that plague other
approaches.