6.837 F98 Lecture 17:
November 12, 1998
Conservative Visibility
Algorithms
Last time we saw several
elegant object-precision or hybrid algorithms
However, difficult to justify
superlinear processing when models get huge.
Let's review the visibility
questions we posed last time:
-
How can invisible scene primitives
be eliminated efficiently? Or...
-
How can visible scene primitives
be identified efficiently? Or...
-
How can hybrid/alternative
versions of the problem be posed? (Later.)
What are tradeoffs among
the methods we saw last time?
Parameters:
model
size n, screen resolution r = w * h
Desiderata:
-
Object precision (continuous) or
screen precision (discrete framebuffer)?
-
Running time
-
Storage overhead (over
and above model storage)
-
Working set:
-
memory locations referenced
over interval delta t, worst case
-
basically, how much memory
is required to avoid excessive VM I/O
-
Overdraw (also depth
complexity):
-
how many times a typical pixel
is written by rasterization process

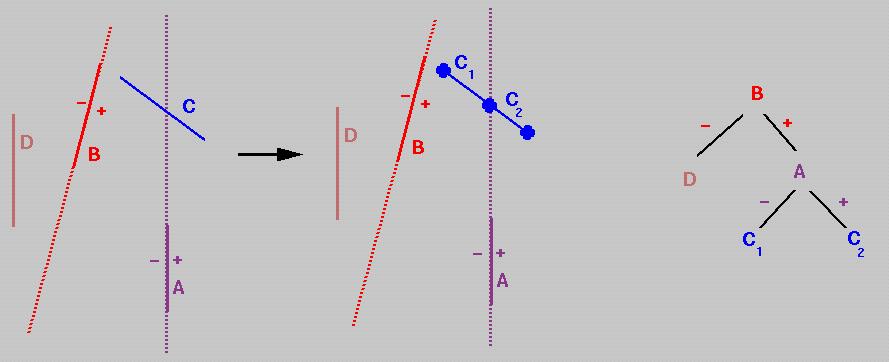
-
Screen-space subdivision
(Warnock's algorithm)
-
Working set size: O(n)
-
Storage overhead: O(n lg
r)
-
Time to resolve visibility
to screen precision: O(n * r)
(though lots of optimizations possible -- worth another
look!)
-
Overdraw: none
-
BSP construction and
traversal (ordering algorithm)
-
Working set size: depends on
definition: O(1), O(lg n)
-
Storage overhead: O(n^2)
-
Time to resolve visibility
to object precision: O(n^2)
-
Overdraw: maximum
-
Z-buffering
-
Working set size: O(1)
-
Storage overhead: O(1)
-
Time to resolve visibility
to screen precision: O(n)
-
Overdraw: maximum
For a time, vanilla clipping
and z-buffering were the best option.
However, soon the O(n) term itself became intolerable. So...
The notion of conservative
visibility oracles arose:
Prefix
pipeline with data structure & algorithm which efficiently
discards invisible polygons,
and/or identifies visible polygons
Assume
an ordinary z-buffered pipeline handles rendering
(that is, resolves visibility at screen resolution -- no fragments)
But:
if oracle is to get the correct picture, what constraint
must it observe? This is called conservative culling.
Example conservative
visibility oracles:
-
Report whole model visible
every frame
-
Cost?
-
Satisfies superset criterion?
By how much?
-
Use analytic solution from
last lecture (e.g.,
report exactly the set of visible fragments)
-
Cost?
-
Satisfies superset criterion?
By how much?
-
BSP tree
-
Is it a visibility oracle?
Is there an algorithmic "middle
ground" between these two extremes?
Early conservative visibility
oracle: hierarchical frustum culling (Garlick et al.,
1990)
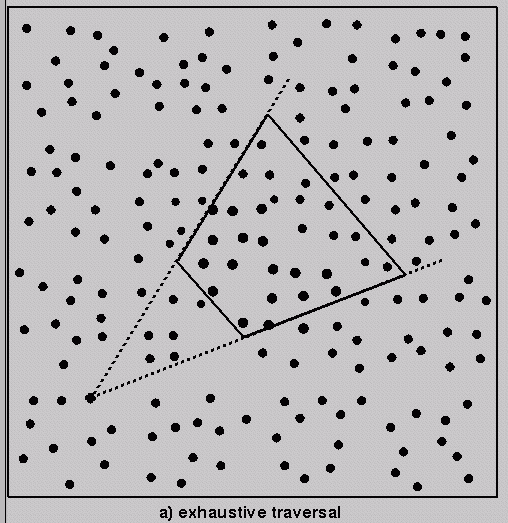
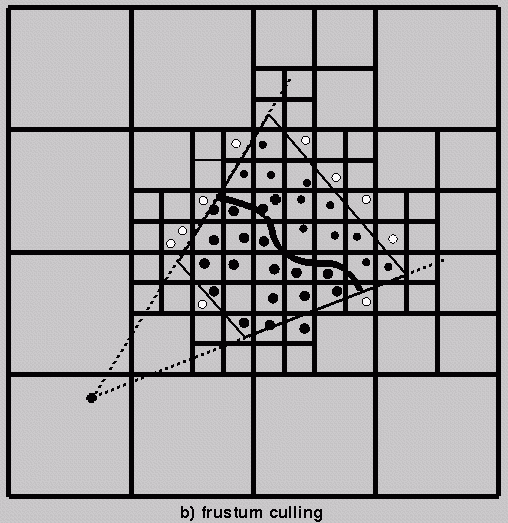
Pseudocode:
Cull (Frustum F, Tree T)
{
if (
F ^ T != null ) { // if F and T are not spatially disjoint
if ( T is a leaf )
render portion of T's contents within F // how ?
else { // examine subtrees (e.g., positive, negative halfspaces)
Cull ( F, T->lochild )
Cull ( F, T->hichild )
}
} // if F ^ T ...
} // Cull
Reduces overdraw somewhat,
on average (for example beyond far
clipping plane) but does not detect occlusion
of one polygon by another
(For
what kind of models/scenes would this algorithm
be ideal -- about as well as you can do?)
... and there can be a whole
lot of occlusion !

UC Berkeley Soda Hall

Typical interior office, with lighting

Same office, with polygon mesh shown
Idea for architectural scenes:
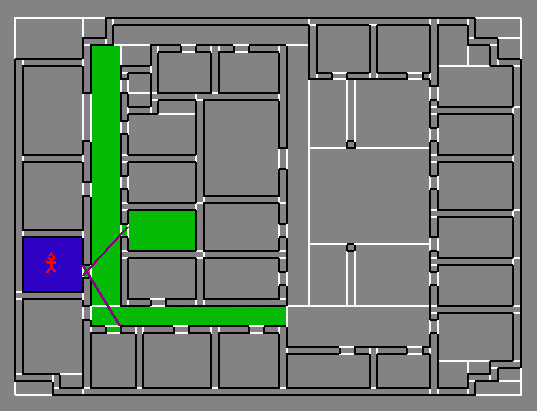
partition model into cells and portals (Jones, 1971)
Schematic (2-D) architectural
model (assume detail objects tagged as such).
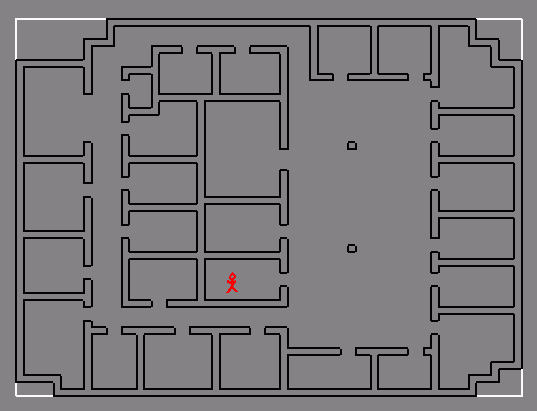
Intuitively: subdivide along
major structural elements (walls, floors, ceilings)
X split: 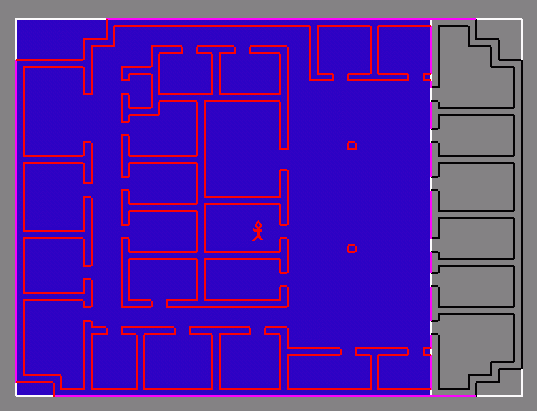 Y split:
Y split: 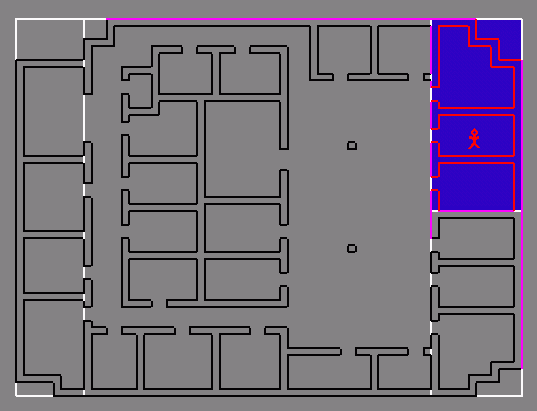
Termination (why)? 
The cells are the
regions at the leaf of the spatial subdivision
The portals are the
non-opaque portions of each cell boundary
Abstraction: convexity,
location, portals, adjacency graph

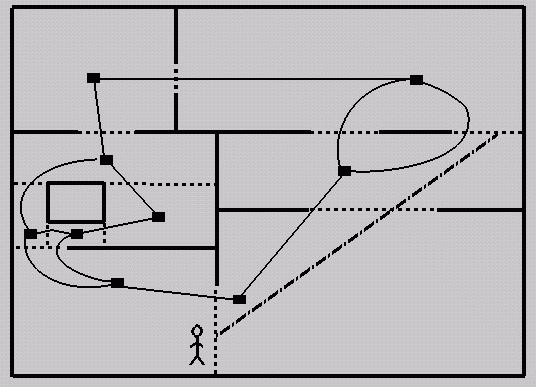
Once the spatial subdivision
"conforms" to this abstraction we can
begin to ask questions about
conservative visibility.
For example: what objects
are potentially visible from a cell
without
regard to instantaneous position of observer (Airey, 1990)?


Store a PVS with each
cell; then render it (subject to frustum culling) interactively.
Later, other researchers
established visibility hierarchically:
First,
between cells:
Then,
iff cell-cell visibility established, between cell and objects
(Later,
see application of inter-object visibility as well)
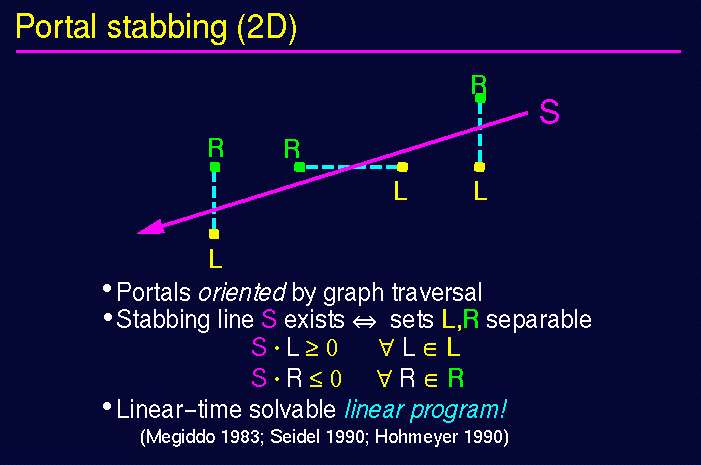
How does this work computationally?
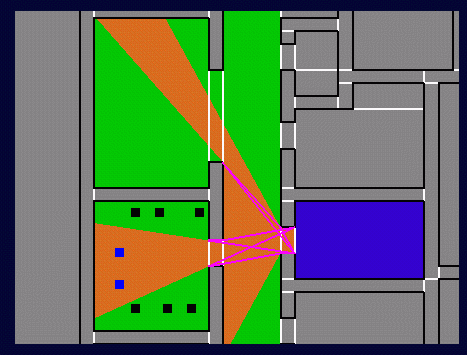
First,
it's sufficient to establish visibility from cell portals (why?)
Second,
the abstract operation of traversing a portal orients the
portal (how?)

Now consider searching outward
into cell adjacency graph
What is the
constraint that truncates the visibility search?
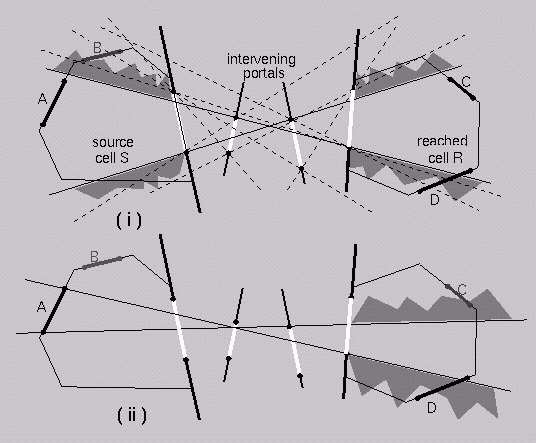
Inter-cell visibility <=>
existence of a sightline which "stabs" the portal sequence
This establishes the existence
of visibility links between cells:

However, we can do better
by establishing cell-to-region visibility (how?):
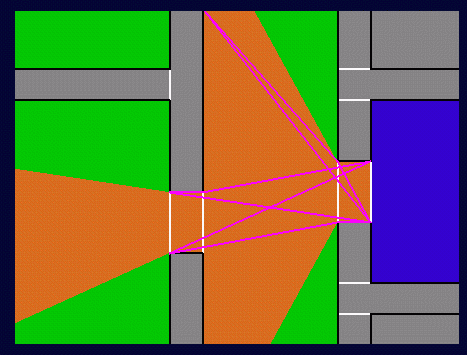
And, within these regions,
potentially visible objects:
(still
without regard to position of observer!)

All of the above can be done
offline (or, perhaps better, lazily -- how?).
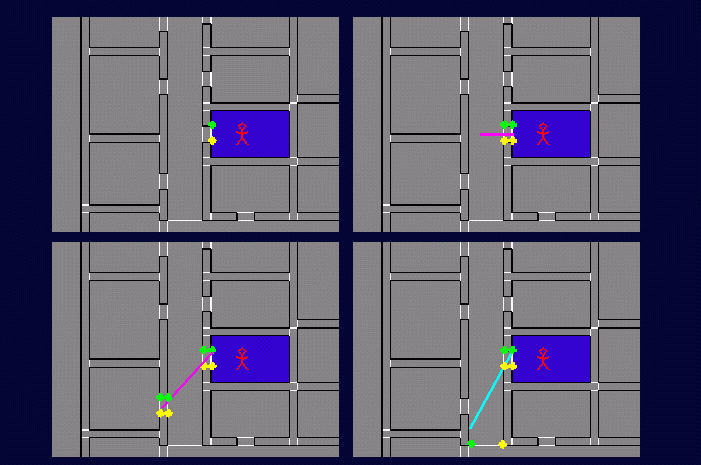
Now we introduce an interactive
query, in which the user's instantaneous
position is
tracked, and his/her view is rendered rapidly (> 10 Hz)
What new information do we
have about the user?
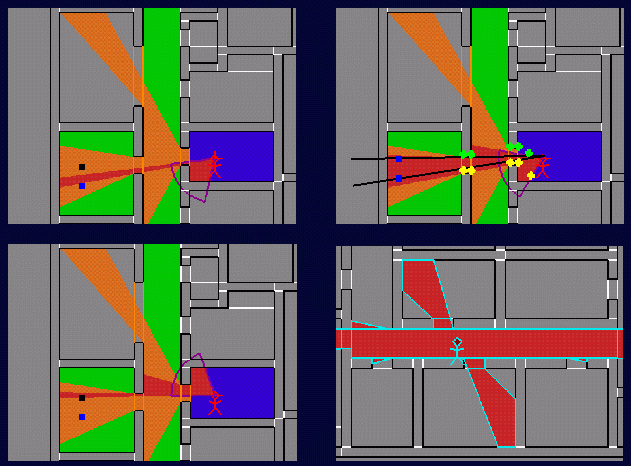
How are eye-to-cell sightlines
established in 2D?
In fact, everything above
works in 3D as well:
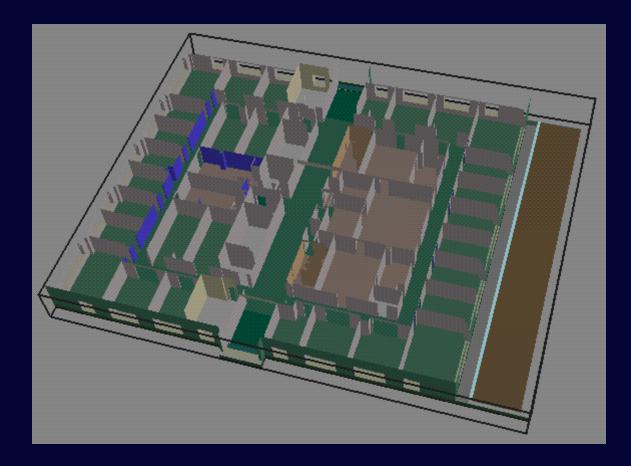
5th Floor of Soda Hall (Structural
Elements)

5th Floor of Soda Hall (Structural
& Detail Element Bounding Boxes)

5th Floor of Soda Hall (Structural
& Detail Elements -- Actual)

With Spatial Subdivision
(Cells and Portals)
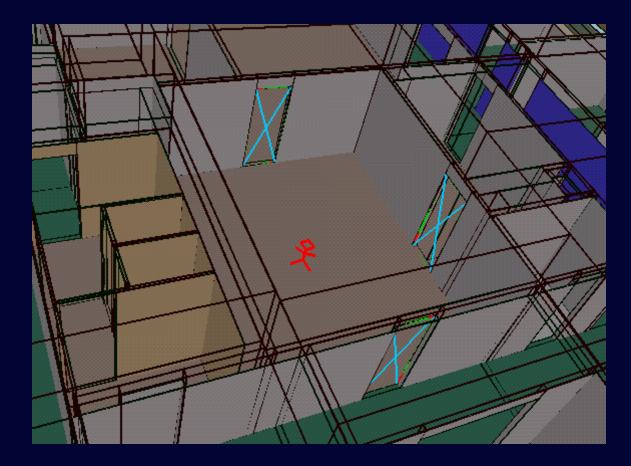
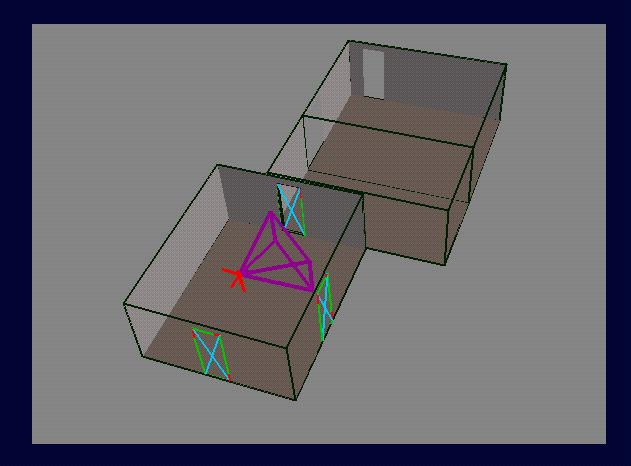
Detail View of a Cell and
its Portals
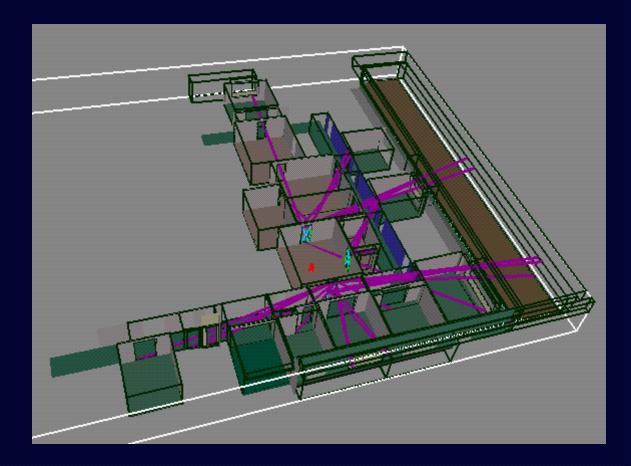
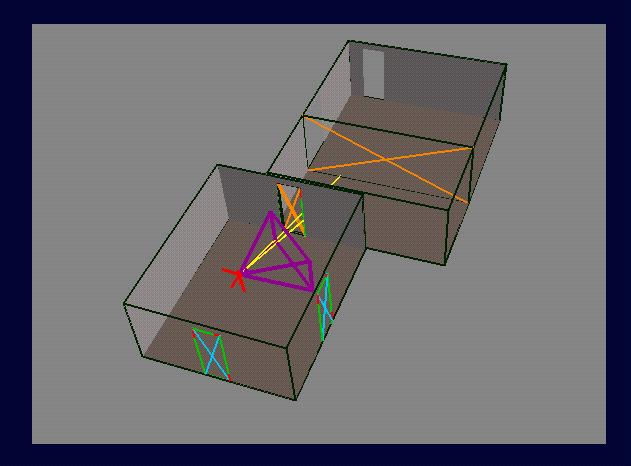
Cell-to-Cell Visibility for
One Cell
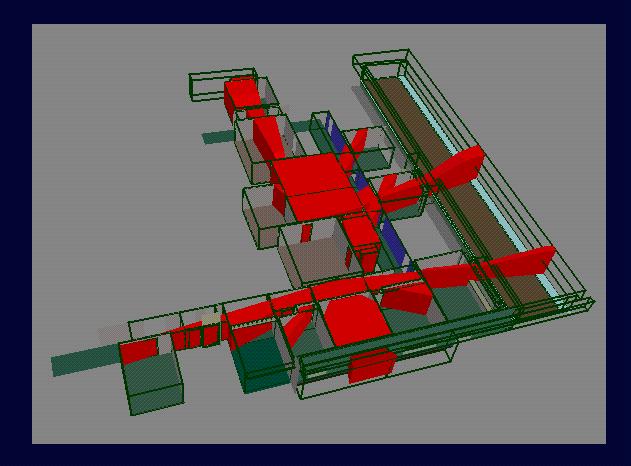
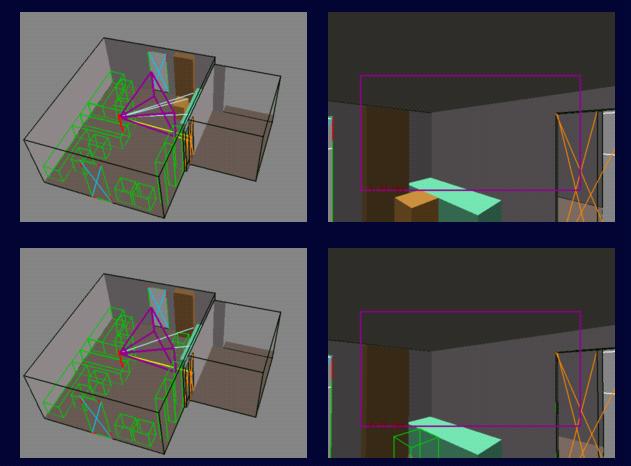
Cell-to-Region Visibility
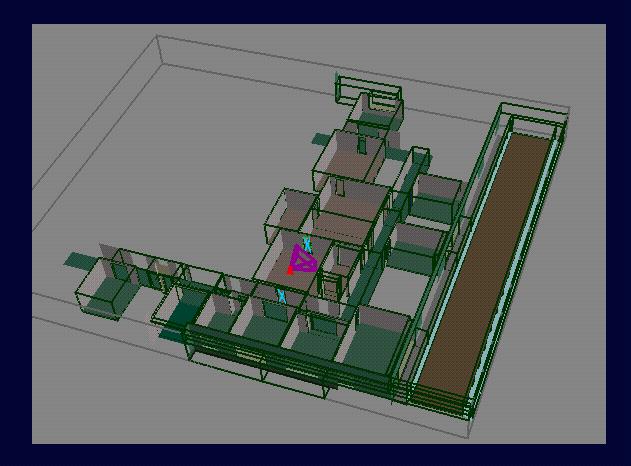
Interactive Query (Observer
Position, Field of View Known)
Detail View
Eye-to-Cell Sightlines Determined
by Linear Programming
How are eye-to-cell sightlines
established in 3D?
Potentially Visible Objects
(Wireframe) and In-Frustum Objects (Shaded)
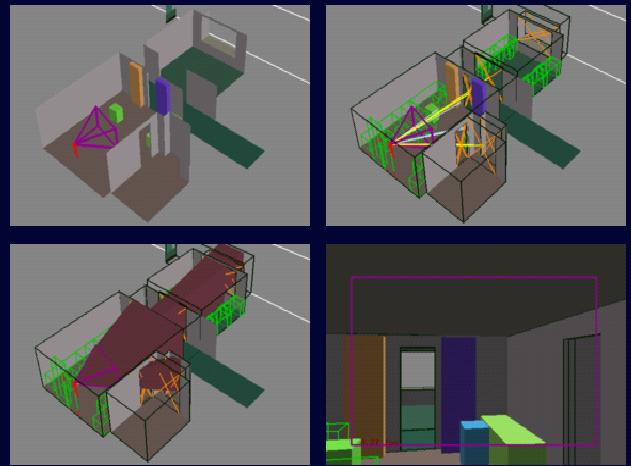
View Through a Series of
Portals
This technique is very effective
for architectural interiors; it was quickly
coded
into commercial CAD packages, games (e.g., Quake et al.)
(though
not too well: "level compilation" is completely unnecessary)
It has another benefit:
one can upper bound the set of geometry that
will
be needed for the next frame, or several frames (why useful?)
But: what happens for
outdoor environments?
Urban
regions
Forests/natural
scenes
Or simply very complex assemblies?
Mechanical
CAD parts (engine blocks, Boeing 777s)
Molecular
visualization
This is a very hard and
still unsolved problem.
A variety of proposed algorithms
exist:
Hierarchical
Z-buffers
Hierarchical
Occlusion Culling
Hierarchical
Occlusion Maps
Read the last few years'
issues of Siggraph, Presence,
and the
ACM Symposium on Computational Geometry.
But all have serious drawbacks
which prevent their widespread adoption.
So the book is still very
much open on this fundamental problem !
Previous
Meeting .... Next Meeting ... Course
Page
Last modified: Nov 1998
Prof. Seth Teller, MIT Computer
Graphics Group, seth@graphics.lcs.mit.edu



































