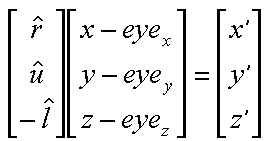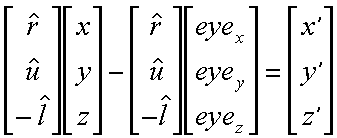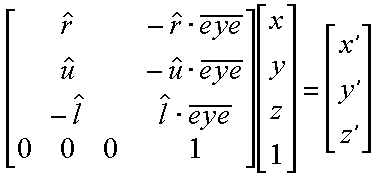Viewing Transformations

After the modeling transformation stage of the rendering pipleine all of the obeject in the scene have been placed within a common coordinate system commonly called world space.

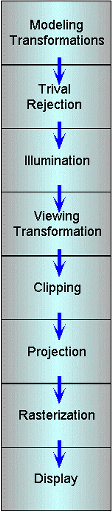
For the moment we are going to skip over the trivial rejection and illumninations stages and consider the view transformation stage. Remember that purpose of the viewing transformation is to orient the objects in a coordinate system where the center of projection is located at the origin. This coordinate system is called either eye space or camera space.

Let's consider an example.

In the scene above the origin of world space is shown as a blue coordinate frame located under the chair. This was a convenient coordinate system for orienting the floor and walls (Notice how the axes are aligned with the floor tiles). The chair and teapot could also be easily placed and oriented in this coordinate system.

The next thing we'd like to do is specify the image of our model that we desire. We'll find this to be much easier when the origin of our coordinate system coincides with the camera as shown below.

The mechanics of this specification can be expressed using the rigid body transformations given in the last lecture. First, we need to perform the rotations needed to align the two coordinate frames.

Then we need to perform a translation that will move the origin of our world space to the camera's origin.

Why did we rotate first? Could we have done it the other way around?

While we have all the tools that are required to specify a viewing transformation. This approach is not very intuitive.

Instead of specifying a desired view as a rotation followed by a translation, we could use the following parameterization. Suppose that we identify the point where the camera is located (in world space), and call it the eye point. Then we identify some world-space point in the scene that we wish to appear in the center of our view. We'll call this point the look-at point. Next, we identify a world space vector that we wish to be oriented upwards in our final image, and this point we'll call the up-vector.

This parameterization is very natural. We can use it to specify an arbitrary camera path by change only the eye-point and leaving the look-at and up vectors untouched. Or we could pan the camera from object to object by leaving the eye-point and up-vector fixed and changing only the look-at point.

Now let's consider how, given such specification, we can synthesize the desired transform.

As disscossed above we will compute the rotation part of the viewing transfromation first. Fortunately, we know some things about the matrix that we are looking for.

For instance, consider a vector along the look at direction:

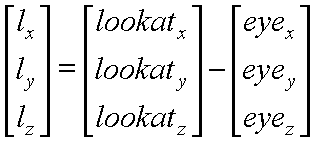
After normalizing it

We expect that our desired matrix will transform it to the vector [0, 0, -1]T (Why?).
There is also another special vector that we can compute. If we find the cross product between the look-at vector with our up vector, we will get a vector that points to the right.
We expect that this vector when normalized will transform to the vector [1, 0, 0]T.
Finally from these two vectors we can sythesize a third vector.
And this vector, when normalized, should transform to [0, 1, 0]T.
Now lets consider all of these results together.
Note that each of our vectors are unit length (i.e. they are normalized) and they are orthogonal to each other (i.e. the projection of any vector onto the other two vectors is zero). Therefore, the matrix is orthonormal, like a rotation matrix. Remember that orthonormal matrices have the unique property that:
And we can solve for the rotation component of the viewing transformation by multiplying both sides by the inverse of the 3 x 3 matrix of vectors that we have computed.

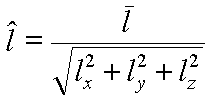
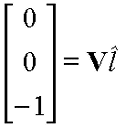
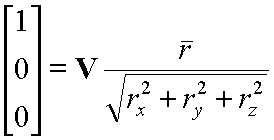
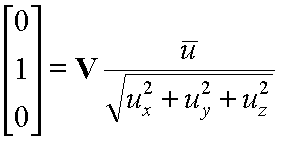
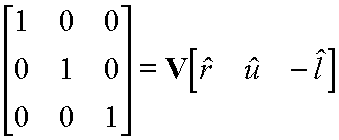
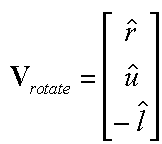
Next we need to compute the translation part of the viewing transformation. We know that we want to apply the rotation that we just derived about the eye point. However, rotations are defined to take place about vectors originating form the origin. We can have our rotation occur about the correct point if we first subtract the coordinate of the eye point from the given world space point that we are transforming into eye-space.

We can simplify this equation to isolate the rotation and translation parts.
We can then convert our transformation to homogeneous coordinates giving us the final version of V.
This page last modified Monday, October 21, 1996