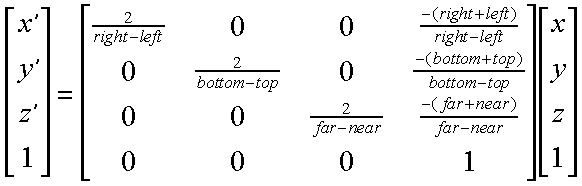There are many different types of projection. The simplist, is to simply ignore the z-dimension. This form of projection is called orthographic or parallel. It is the common form of projection used by draftspeople for top, bottom, and side views. The advantage of parallel projection is that the you can make accurate measurments of image features in the two dimensions that remain. The disadvantage is that the images don't appear natural (i.e. they lack perspective foreshorting).
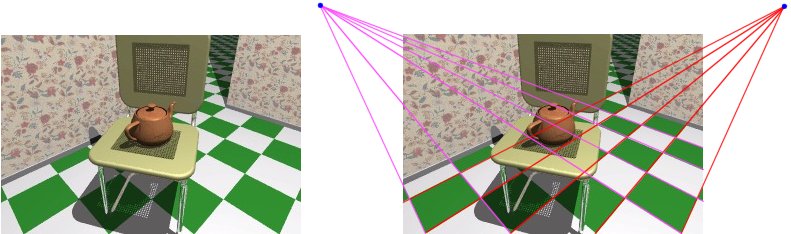
Here is an example of an parallel projection of our scene.

The projection matrix for orthographic projection is very simple
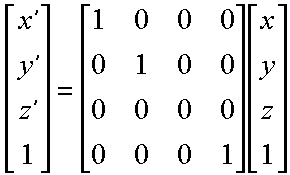
There are someproblems with this simple form, however. To begin with the units of the transformed points are still the same as the model. This is great for drafting, but in our case we'd like for the units to be in pixels.
We can incorporate this change of units, and perform the flip of the y-axis required for raster coordinates into our projection matrix as follows.
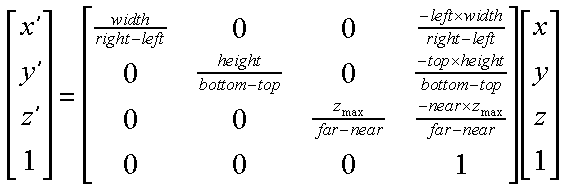
For realistic three-dimensional viewing we'd like for our objects to be displayed with proper perspective. Perspective causes objects nearer to the viewing poisition to appear larger that the same object would when place farther from the viewpoint.
Artists (Donatello, Brunelleschi, and Da Vinci) during the renaissance discovered the importance of perspective for making images appear realistic. This outdates mathematicians by more than 300 years. The real reason for introducing homogenous, or projective coordinates to computer graphics was to accomplish perspective projections using linear operators. Not, as mentioned earlier, for comnbining rotations and translations in the same framework.
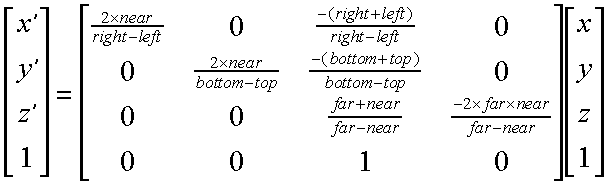
Lets start by looking at a perspective projection.

Note how lines known to be parallel in image space appear to converge to intersect when viewed in perspective.
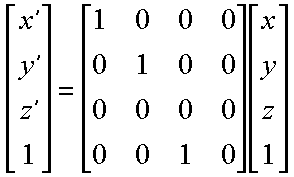
Notice how similar this transform is to the original parallel projection. It also has all of the disadvantages of the parallel form, its units are not screen space units. The following transformation accomplishs the projection and the conversion to pixels in a single transform.
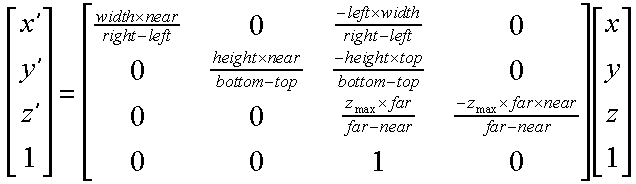
For the purpose of clipping we can modify this transformation so that it is mapped into a canonical space. Following is a canonical space mapping for orthographic projections.