The complication of clipping is computing the new vertices. This process is greatly simplified by using a canonical clipping volume. We mentioned in the last lecture that it is often desireable to introduce an intermediate coordinate frame in-between the eye space and the viewport space. In the canonical space the viewable region is projected into a volume that ranges from -1 to +1 in all dimensions. Therefore, in homogeneous coordinates, before the division by w,  coordinates in all dimensions range from -w to +w.

After division	Before Division (Homogenous)

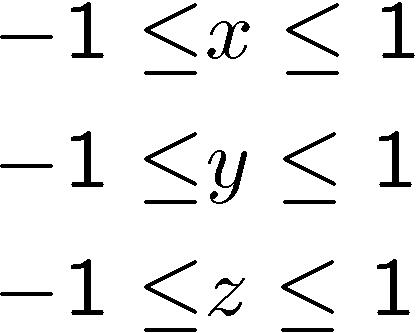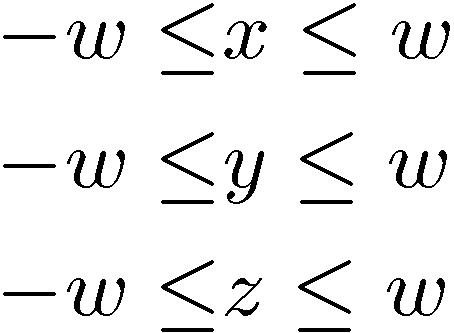The canonical space in homogenous coordinates has several advantages. It simplifies the clipping test (all dimensions are compared against the w component of the vertex) and it is the perfect place in the pipeline to transistion from a floating-point to a fixed-point representation.