Frames
We will accommodate this difference between the spaces that points live in
and the spaces that vectors live in our basis definition. We will call the
spaces that points live in Affine spaces, and explain why shortly.
We will also call affine-basis-sets frames.
In order to use this new basis, we will need to adjust our coordinates. Noting that
the origin component of our is a point, and remembering from our previous discussion,
that it makes no sense to multiply points by arbitrary scalar values, we arrive at the following
convention for giving points (and vectors) coordinates:
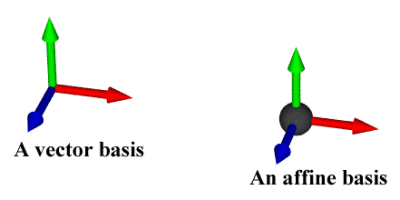
Graphically, we will distinguish
between vector bases and affine
bases (frames) using the convention shown
on the left.
|
|