At this stage, you're probably comfortable thinking of 3D
points, and 3D vectors as being represented by 3 numbers.
For instance:
This representation is, however, horribly underspecified. Implied in this notation is
an agreed upon coordinate system.
This coordnate system has an agreed upon set of directions, and an
agreed upon origin.
If we change coordinate systems, our representation (set of numbers) changes. If we
move points relative to our coordinate system, our representation also changes.
In order to understand and affect these changes we will make our representation more explicit.
|
We start by defining some notation:
- Points will be denoted as
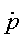
- Vectors will be denoted as

- Coordinates are denoted as c
(a lower-case boldface variable).
These are those numbers we are so fond of.
- Coordinate Systems are denoted as
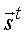
We will deal with two different types of coordinate systems:
A coordinate basis defines vectors.
A coordinate frame defines points.
Thus, a completely specified point looks like:
(If this is unclear, we'll get back to it in a couple of slides)
|