E.M. Rauch
![]() , H. Sayama
, H. Sayama![]() and Y. Bar-Yam
and Y. Bar-Yam
![]()
PACS numbers: 87.23.Kg, 87.23.Cc, 89.75.Fb
The work of Fisher, Haldane and Wright [1] established the generation-to-generation
change in frequency of genotypes as a measure of fitness characterizing the
role of natural selection in evolution. The centrality of this characterization
[2] has not been diminished by recognized observational difficulties
due to sampling error, the intricacies of the genotype-phenotype relationship,
and the possibility of environmental changes. The measure most often used to
quantify fitness of a type is the net reproduction ratio ![]() , the expected
number of surviving offspring per organism over its lifetime (in an environment with other individuals and species present), or its differential analogue, the ``Malthusian parameter''
, the expected
number of surviving offspring per organism over its lifetime (in an environment with other individuals and species present), or its differential analogue, the ``Malthusian parameter'' ![]() . The concept of
invasibility is another approach to the question of what types will come to
dominate a population. One considers a population dominated by a type
. The concept of
invasibility is another approach to the question of what types will come to
dominate a population. One considers a population dominated by a type ![]() and asks whether a mutant type
and asks whether a mutant type ![]() can invade. An evolutionarily
stable strategy[5] is one for which no mutant can invade. Under the
assumptions normally used, the evolutionarily stable strategy is the one that
maximizes
can invade. An evolutionarily
stable strategy[5] is one for which no mutant can invade. Under the
assumptions normally used, the evolutionarily stable strategy is the one that
maximizes ![]() [6]. The assumption that populations that have reached a stationary state will
be composed mainly of types with the highest number of offspring only applies
to systems where the instantaneous change in frequency is sufficient to determine
the long-term composition of the population.
Conditions such as frequency-[3] and density-dependent[4] selection provide contexts in which this measure does not predict the fate of a type before equilibrium has been reached.
In this paper, we use a simple
spatially-extended predator-prey or host-pathogen model [7,8,9,10]
to show a more direct departure from this characterization. We first reproduce the results obtained by others using similar models and then
extend these results by studying the time-dependent fitness of strains. We then
present our conclusions, which have been qualitatively anticipated, but are
first quantified here. In the model, the evolutionarily stable type is out-competed
in the short term by seemingly fitter mutants. These mutants enjoy high reproduction
ratios for many generations, but go extinct in the long term (e.g. after 200
generations). The rapidly-reproducing types modify their local environment in
a way that is detrimental to their survival, but this environmental modification
and its feedback to population growth requires many generations. The distinct
fates of the different types are made possible by self-organized spatial segregation.
We will define a more general measure of invasion fitness that acknowledges
that descendents may have different reproductive success than their ancestors
of the same type. This measure indicates the evolutionarily stable type in such
cases, and it can be used to quantify the time scale at which selection acts
against the mutants with short-term advantage.
[6]. The assumption that populations that have reached a stationary state will
be composed mainly of types with the highest number of offspring only applies
to systems where the instantaneous change in frequency is sufficient to determine
the long-term composition of the population.
Conditions such as frequency-[3] and density-dependent[4] selection provide contexts in which this measure does not predict the fate of a type before equilibrium has been reached.
In this paper, we use a simple
spatially-extended predator-prey or host-pathogen model [7,8,9,10]
to show a more direct departure from this characterization. We first reproduce the results obtained by others using similar models and then
extend these results by studying the time-dependent fitness of strains. We then
present our conclusions, which have been qualitatively anticipated, but are
first quantified here. In the model, the evolutionarily stable type is out-competed
in the short term by seemingly fitter mutants. These mutants enjoy high reproduction
ratios for many generations, but go extinct in the long term (e.g. after 200
generations). The rapidly-reproducing types modify their local environment in
a way that is detrimental to their survival, but this environmental modification
and its feedback to population growth requires many generations. The distinct
fates of the different types are made possible by self-organized spatial segregation.
We will define a more general measure of invasion fitness that acknowledges
that descendents may have different reproductive success than their ancestors
of the same type. This measure indicates the evolutionarily stable type in such
cases, and it can be used to quantify the time scale at which selection acts
against the mutants with short-term advantage.
As an example of a system with different short-term and long-term fitness, we
use a simple spatially-extended model of a parasite or pathogen spreading through
a host population[8,9]. The model can also be thought of
as a predator-prey system, with the pathogens being predators and the hosts
prey[10,11]. Such systems exhibit interesting spatial
dynamics which are not present in the mean-field approximation; hence, space
is fundamental to their dynamics, a property believed to be shared by many real
biological systems [12,13]. The model is a probabilistic cellular automaton,
with possible states ![]() (empty),
(empty), ![]() (susceptible host), and
(susceptible host), and ![]() (host infected with pathogen of transmissibility
(host infected with pathogen of transmissibility ![]() ). It has three
parameters. At each time step, susceptible hosts reproduce into each neighboring
cell with probability
). It has three
parameters. At each time step, susceptible hosts reproduce into each neighboring
cell with probability ![]() if that cell is not yet occupied; the
probability of reproduction is independent for each neighbor. An infected host
dies with probability
if that cell is not yet occupied; the
probability of reproduction is independent for each neighbor. An infected host
dies with probability ![]() (virulence). Finally, an infected host
(virulence). Finally, an infected host
![]() causes a neighboring uninfected host to become infected with
probability
causes a neighboring uninfected host to become infected with
probability ![]() . In predator-prey language,
. In predator-prey language, ![]() is the prey reproduction
rate,
is the prey reproduction
rate, ![]() describes the rate of predation, and
describes the rate of predation, and ![]() describes the
rate of migration or dispersal to neighboring sites. The subscript
describes the
rate of migration or dispersal to neighboring sites. The subscript ![]() allows more than one type to be present on the lattice. The state transition
probabilities are:
allows more than one type to be present on the lattice. The state transition
probabilities are:
| (1) |
where ![]() is the number of uninfected host neighbors, and
is the number of uninfected host neighbors, and ![]() is the number of infected neighbors of transmissibility
is the number of infected neighbors of transmissibility ![]() . The lattice
is updated synchronously, as the dynamics are not significantly different when
updating asynchronously[8]. When all pathogen individuals are of the
same type, the model reduces to the predator-prey model studied in [10]
except that the probabilities of any two neighbors of a site sending offspring
to that site are independent of each other (and if more than one neighbor sends
offspring to the site, the parent is chosen at random), rather than being linear
in the number of neighbors. However, this difference does not significantly
affect the dynamics. The model differs more fundamentally from the forest fire
model[14] and other models of excitable media[15]:
growth of susceptible hosts occurs locally rather than uniformly in space.
. The lattice
is updated synchronously, as the dynamics are not significantly different when
updating asynchronously[8]. When all pathogen individuals are of the
same type, the model reduces to the predator-prey model studied in [10]
except that the probabilities of any two neighbors of a site sending offspring
to that site are independent of each other (and if more than one neighbor sends
offspring to the site, the parent is chosen at random), rather than being linear
in the number of neighbors. However, this difference does not significantly
affect the dynamics. The model differs more fundamentally from the forest fire
model[14] and other models of excitable media[15]:
growth of susceptible hosts occurs locally rather than uniformly in space.
In a mean field approximation [8], the growth rate of a type monotonically
increases with ![]() . Thus, in homogeneous systems with competing strains,
higher-
. Thus, in homogeneous systems with competing strains,
higher-![]() strains dominate[16]. The mean-field approximation
does not capture interesting aspects of the spatial variation in this model.
The densities of host and pathogen fluctuate locally[10]. The
system as a whole can have one of the following outcomes: the pathogen dies
out but the host survives, host and pathogen coexist, or the pathogen drives
the host to extinction. Parasite-driven extinction occurs above a threshold
of
strains dominate[16]. The mean-field approximation
does not capture interesting aspects of the spatial variation in this model.
The densities of host and pathogen fluctuate locally[10]. The
system as a whole can have one of the following outcomes: the pathogen dies
out but the host survives, host and pathogen coexist, or the pathogen drives
the host to extinction. Parasite-driven extinction occurs above a threshold
of ![]() which depends on the values of the other parameters[17].
which depends on the values of the other parameters[17].
In order to investigate the evolutionary dynamics more fully, we introduce mutation
into the dynamics of the model, as has recently been done in similar models[18,19,9].
The transmissibility becomes a quantitative trait of an individual pathogen.
When a pathogen of transmissibility ![]() reproduces, its offspring has
probability
reproduces, its offspring has
probability ![]() of having transmissibility
of having transmissibility
![]() :
:
![\begin{displaymath}
P(S\rightarrow I_{\tau })=\left[ 1-\prod _{\tau '}(1-\tau ')...
...}p_{\tau ''+\varepsilon }+(1-\mu )p_{\tau ''}\right) }\right]
\end{displaymath}](img23.gif) |
(2) |
where
![]() and
and ![]() is the number of infected neighbors of transmissibility
is the number of infected neighbors of transmissibility ![]() . For suitably
large lattice sizes, the system evolves to an evolutionarily stable average
value of
. For suitably
large lattice sizes, the system evolves to an evolutionarily stable average
value of ![]() [9]. When high values of
[9]. When high values of ![]() lead
to extinction,
lead
to extinction, ![]() does not increase to the point of extinction; rather,
the system reaches an evolutionarily stable value which is lower than the extinction
limit. This is the case for the entire region of parameter space where parasites
and hosts coexist.
does not increase to the point of extinction; rather,
the system reaches an evolutionarily stable value which is lower than the extinction
limit. This is the case for the entire region of parameter space where parasites
and hosts coexist.
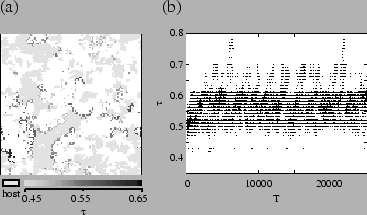
The distribution of ![]() during evolution has significant features that
have not yet been noted. Figure
during evolution has significant features that
have not yet been noted. Figure ![[*]](crossref.png) is a density plot showing
the distribution of
is a density plot showing
the distribution of ![]() over time. In this figure, it is apparent that
strains of pathogens continue to evolve higher
over time. In this figure, it is apparent that
strains of pathogens continue to evolve higher ![]() , but these strains
go extinct. A population of pathogens above the evolutionarily stable value,
but able to coexist with the host, evolves to a lower transmissibility.
, but these strains
go extinct. A population of pathogens above the evolutionarily stable value,
but able to coexist with the host, evolves to a lower transmissibility.
To shed light on the evolutionary dynamics of the system, we will begin by examining
the reproduction ratio for pathogens of different types when mutations are to
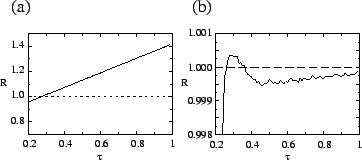
a random transmissibility rather than being a fixed increment. Figure ![[*]](crossref.png) a
shows the net reproduction ratio
a
shows the net reproduction ratio ![]() for mutants when they first
arise; it increases monotonically with
for mutants when they first
arise; it increases monotonically with ![]() . However, figure
. However, figure ![[*]](crossref.png) b
shows
b
shows ![]() for all pathogens, averaged over time. It peaks at the
evolutionarily stable value. Thus, selection favors high-
for all pathogens, averaged over time. It peaks at the
evolutionarily stable value. Thus, selection favors high-![]() mutants
initially, consistent with the spatially homogeneous case. The difference between
these two plots shows that selection against high-
mutants
initially, consistent with the spatially homogeneous case. The difference between
these two plots shows that selection against high-![]() mutants acts
only on longer time scales; evolutionary dynamics are different at different
time scales.
mutants acts
only on longer time scales; evolutionary dynamics are different at different
time scales.
In order to explicitly contrast the fitness at different time scales, we must
consider the reproductive success not only of the mutant, but also of its descendants,
which can vary as a function of time since the beginning of the strain. For
a general evolving system, we define the time-dependent invasion fitness
![]() to be the expected number of descendants at time
to be the expected number of descendants at time ![]() of a mutant of type
of a mutant of type ![]() introduced at time
introduced at time ![]() .
. ![]() can be
measured as time or in generations; here we use the number of generations. Note
that
can be
measured as time or in generations; here we use the number of generations. Note
that ![]() is the net reproduction ratio
is the net reproduction ratio ![]() for mutants. In
general,
for mutants. In
general, ![]() should include environmental factors in its arguments.
When, however, the local environment of type
should include environmental factors in its arguments.
When, however, the local environment of type ![]() is shaped by
is shaped by ![]() itself, as in the model[20], one may write it as a function of only
time and type. In order to make a more explicit comparison with the reproduction
ratio
itself, as in the model[20], one may write it as a function of only
time and type. In order to make a more explicit comparison with the reproduction
ratio ![]() , one can calculate the normalized reproduction ratio as a function
of time
, one can calculate the normalized reproduction ratio as a function
of time
![]() . The evolutionarily stable types
. The evolutionarily stable types ![]() are given by
are given by ![]() such that
such that
![]() .
No other value of
.
No other value of ![]() can successfully invade in the long term.
can successfully invade in the long term.
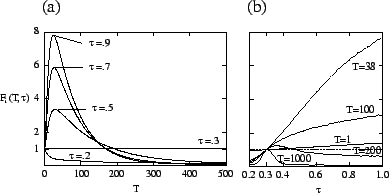
In our model, the type ![]() of the evolving species corresponds to the transmissibility
of the evolving species corresponds to the transmissibility
![]() . Figure
. Figure ![[*]](crossref.png) shows
shows
![]() , obtained numerically
for the host-pathogen model. Strains where
, obtained numerically
for the host-pathogen model. Strains where ![]() is less than the evolutionarily
stable value
is less than the evolutionarily
stable value ![]() have both a short-term and long-term disadvantage,
and decline immediately. Strains with
have both a short-term and long-term disadvantage,
and decline immediately. Strains with
![]() , by contrast,
initially grow much more quickly than those of the evolutionarily stable type,
but begin declining after an average of about 30 generations. Nevertheless,
they remain more successful than the evolutionarily stable type for a large
number of generations. Selection begins to act against strains of a given non-evolutionarily-stable
type when its curve drops below that of the evolutionarily stable type.
, by contrast,
initially grow much more quickly than those of the evolutionarily stable type,
but begin declining after an average of about 30 generations. Nevertheless,
they remain more successful than the evolutionarily stable type for a large
number of generations. Selection begins to act against strains of a given non-evolutionarily-stable
type when its curve drops below that of the evolutionarily stable type.
Using time-dependent fitness, one can determine which types dominate at each
time scale. For a given time scale ![]() , the most successful type for that
time scale
, the most successful type for that
time scale ![]() is the value of
is the value of ![]() such that
such that ![]() is maximized (
is maximized (
![]() ). Systems for which
). Systems for which
![]() have the same short- and long-term fitness. Figure
have the same short- and long-term fitness. Figure ![[*]](crossref.png) a shows that,
for the model, one type dominates for short time scales, and another dominates
for long time scales, with a sharp transition between the two scales. This curve
determine the meaning of ``short-`` and ``long-term'' as we have been using
them.
a shows that,
for the model, one type dominates for short time scales, and another dominates
for long time scales, with a sharp transition between the two scales. This curve
determine the meaning of ``short-`` and ``long-term'' as we have been using
them.
Since selection acts differently on a given type at different time scales, one
can determine the relevant time scales for a particular type. For all ![]() we can define the time scale
we can define the time scale ![]() at which selection acts against
at which selection acts against
![]() as
as
![]() .
Thus for some
.
Thus for some ![]() , mutants of phenotype
, mutants of phenotype ![]() have more descendants
than those of
have more descendants
than those of ![]() . The time scale at which the evolutionarily stable
type begins to dominate is given by
. The time scale at which the evolutionarily stable
type begins to dominate is given by
![]() .
For the host-pathogen system (
.
For the host-pathogen system (![]() ), figure
), figure ![[*]](crossref.png) b shows
b shows ![]() . For
. For
![]() ,
,
![]() since these low-transmissibility
types have a disadvantage on all time scales. For
since these low-transmissibility
types have a disadvantage on all time scales. For
![]() ,
, ![]() approaches a constant number of generations (about 200 for the parameters used
in figure
approaches a constant number of generations (about 200 for the parameters used
in figure ![[*]](crossref.png) b) but is larger when
b) but is larger when ![]() is close to
is close to ![]() .
Thus, for
.
Thus, for
![]() , on time scales significantly shorter than
, on time scales significantly shorter than
![]() , the dynamics of the relative frequencies of different types can
be determined from their values of the net reproduction ratio
, the dynamics of the relative frequencies of different types can
be determined from their values of the net reproduction ratio ![]() ; on longer
time scales, other mechanisms are essential to the dynamics, such as the feedback
between the population and the environment. In general, when a type has a short-term
advantage (
; on longer
time scales, other mechanisms are essential to the dynamics, such as the feedback
between the population and the environment. In general, when a type has a short-term
advantage (
![]() ),
), ![]() is a quantitative measure
of the time scale in which instantaneous change in frequency dominates the evolutionary
dynamics for that type.
is a quantitative measure
of the time scale in which instantaneous change in frequency dominates the evolutionary
dynamics for that type.
Because some of the individuals in the population can be of rapidly-reproducing
types that have high short- but low long-term fitness,
the long-term composition of types in the population cannot necessarily be
given by the types with high long-term fitness plus mutation-selection balance.
Instead, the distribution ![]() of types,
of types, ![]() , is given
for low mutation rates by:
, is given
for low mutation rates by:
![\begin{displaymath}
P(p)=\frac{n(p)\int _{T=0}^{\infty }F_{i}(T,p)}{n_{es}+\sum ...
..._{es}}n(p' )\left[ \int ^{\infty }_{T=0}F_{i}(T,p' )\right] }
\end{displaymath}](img54.gif) |
(3) |
where ![]() is the rate at which mutants of type
is the rate at which mutants of type ![]() arise,
and
arise,
and ![]() is the average number of individuals of the evolutionarily
stable type.
is the average number of individuals of the evolutionarily
stable type. ![]() for the model measured numerically agrees with the above (except
for types which are within 0.1 of the evolutionarily stable type, since these
strains take a long time to decline and were not tracked longer than 1000 generations).
for the model measured numerically agrees with the above (except
for types which are within 0.1 of the evolutionarily stable type, since these
strains take a long time to decline and were not tracked longer than 1000 generations).
The tendency to spatial segregation of different strains can be seen in fig.
![[*]](crossref.png) . Although different strains are always coming in contact, pathogens
tend to be surrounded by those of similar type. This results from local reproduction
and local extinction of higher-
. Although different strains are always coming in contact, pathogens
tend to be surrounded by those of similar type. This results from local reproduction
and local extinction of higher-![]() strains. Mutation causes individuals
of a range of types to arise for selection to act on; since these types are
segregated spatially, selection can be viewed as acting on clusters of organisms
associated by spatial proximity.
strains. Mutation causes individuals
of a range of types to arise for selection to act on; since these types are
segregated spatially, selection can be viewed as acting on clusters of organisms
associated by spatial proximity.
A connection has been made between spatially inhomogeneous models and group selection and/or ``altruism''. Such a connection can be loosely justified; however, while strict individual selection is a restrictive limit of evolving systems, the dichotomy of group and individual selection also does not capture the richness of spatial populations. Typically, in our model, neither the spatial groups nor the genetically related groups nor structures of spatial patterns (e.g. spiral waves in reference [21]) are clearly determinable. Rather than focusing on the distinction or balance between group and individual selection, we have focused on the multi-generational fitness of strains as a dynamic property of organisms in spatially inhomogeneous environments.
Since organisms often greatly affect their own environment, the feedback between the environmental change caused by the organism and selection may be substantial[2]. The model demonstrates one possible mechanism for this feedback: the local depletion of the resource by organisms is ultimately detrimental to their survival. The contrast between long-term and short-term fitness may characterize other systems which have the general property that a population depends on, and can deplete, a resource that grows locally, and where reproduction is local. If mutations are frequent, such a system observed in nature may contain a significantly different distribution of organism types than would be expected if selection acts only at one time scale. It is more appropriate to view the composition of types in such systems as a mixture of types, each of which is adapted to a particular time scale.
Acknowledgement: This work is supported in part by the National Science Foundation under Grant No. 0083885.
|
|
|
Erik Rauch 2002-05-27