Also on fractals: A Fractal Brownian Archipelago
Lacunarity is a counterpart to the fractal dimension that describes the texture of a fractal. It has to do with the size distribution of the holes. Roughly speaking, if a fractal has large gaps or holes, it has high lacunarity; on the other hand, if a fractal is almost translationally invariant, it has low lacunarity. Different fractals can be constructed that have the same dimension but that look widely different because they have different lacunarity. There are applications of lacunarity in image processing, ecology, medicine, and other fields.
The properties and characteristics of a fractal set are not completely
determined by its fractal dimension D. Indeed, it is easy to construct
a family of fractals that share the same D but differ sharply. As
an example of such a construction, the above depicts a stack of Cantor
sets made up by a generator of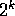 
intervals and a reduction factor 
.
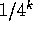By construction, all have the same fractal dimension 
.
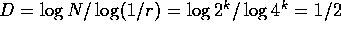Starting from the upper middle set, the index k varies from 1
to 6 when moving up and 1 to 5 when moving down. Below
the middle, the
segments are
uniformly distributed; above, they are closely packed at the ends of the
set. The extremes do not look "like fractals": the one in the bottombegins
to resemble a filled interval, while the one on the top looks
like two isolated points at the ends of the set. Only the central Cantor
set looks like a true fractal.
These sets have different "texture", more specifically, different lacunarity. Lacunarity is a notion distinct and independent from D; it is not related with the topology of the fractal and needs more than one numerical variable to be fully determined. Lacunarity is strongly related with the size distribution of the holes on the fractal and with its deviation from translational invariance; roughly speaking, a fractal is very lacunar if its holes tend to be large, in the sense that they include large regions of space.
An expanded version more appropriate for physicist is found in
Mandelbrot BB. "Measures of fractal lacunarity:
Minkowski content and alternatives".Fractal
Geometry and Stochastics eds C Bandt, S Graf, and M Zähle
(Basel and Boston: Birkhäuser Verlag), 1995.
Blumenfeld
R, Mandelbrot BB. Levy dusts, Mittag-Leffler statistics,
mass fractal lacunarity, and perceived dimension. Physical Review
E. Statistical Physics, Plasmas, Fluids, & Related Interdisciplinary
Topics, vol.56, no.1, pt.B, July 1997, pp.112-18.
Plotnick RE, Gardner RH, Hargrove WW, Prestegaard K, Perlmutter M. Lacunarity analysis: a general technique for the analysis of spatial patterns. Physical Review E. Statistical Physics, Plasmas, Fluids, & Related Interdisciplinary Topics, vol.53, no.5, pt.B, May 1996, pp.5461-8.
Hovi J-P, Aharony A, Stauffer D, Mandelbrot BB. Gap independence and lacunarity in percolation clusters. Physical Review Letters, vol.77, no.5, 29 July 1996, pp.877-80.
Smith LA, Fournier JD, Spiegel EA. Lacunarity and intermittency in fluid turbulence. Physics Letters A 114: (8-9) 465-468 Mar 17 1986.
Solis FJ, Tao L. Lacunarity of random fractals. Physics Letters A 228: (6) 351-356, 21 April 1997.
Plotnick RE, Gardner RH, Oneill RV. Lacunarity indexes as measures of landscape texture. Landscape Ecology 8: (3) 201-211 Sep 1993.
Einstein AJ, Wu HS, Gil J. Self-affinity and lacunarity of chromatin texture in benign and malignant breast epithelial cell nuclei. Physical Review Letters 80: (2) 397-400 Jan 12 1998.
Mandelbrot BB, Vespignani A, Kaufman H. Crosscut analysis of large radial DLA: departures from self-similarity and lacunarity effects. Europhysics Letters, vol.32, no.3, 20 Oct. 1995, pp.199-204.
Obert M. Numerical estimates of the fractal dimension D and the lacunarity L by the mass radius relation. [Conference Paper] Fractals-An Interdisciplinary Journal on the Complex Geometry of Nature, vol.1, no.3, Sept. 1993, pp.711-21.
Gefen Y, Meir Y, Mandelbrot BB, Aharony A. Geometric
implementation of hypercubic lattices with noninteger dimensionality by
use of low lacunarity fractal lattices. Physical Review Letters,
vol.50, no.3, 17 Jan. 1983, pp.145-8.
Erik Rauch
