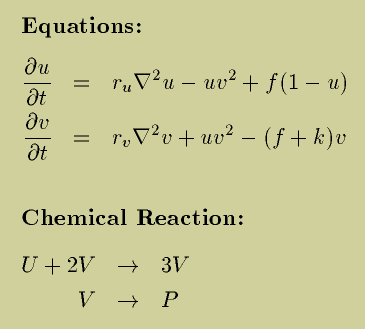Gray Scott Model of Reaction Diffusion
Abelson, Adams, Coore, Hanson, Nagpal, Sussman
Reaction and diffusion of chemical species can produce a variety of
patterns, reminiscent of those often seen in nature. The Gray Scott
equations model such a reaction. For more information on this
chemical system see the articles "Complex Patterns in a Simple
System," by John E. Pearson and "Pattern Formation by Interacting
Chemical Fronts," by K.J. Lee, W.D. McCormick, Qi Ouyang, and
H.L. Swinney. These articles appeared in Science, Volume 261,
9 July 1993.
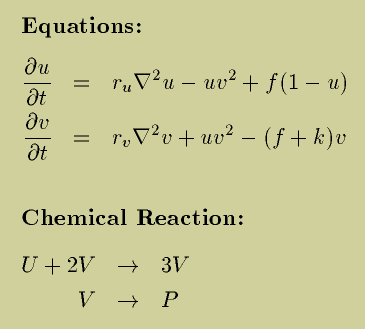
U and
V and
P are chemical species.
u and
v represent their concentrations.
ru and
rv are their diffusion rates.
k represents the rate of conversion of V to P.
f represents the rate of the process that feeds U
and drains U,V and P.
|
|
The partial differential equations modeling this process may be
simulated with a variety of numerical techniques. One may expect good
results with even such crude methods as forward Euler integration of
the finite-difference equations that one obtains by spatial
discretization of the Laplacian.
One may also simulate the underlying
process, which is stoichiometrically conservative (accounting for the
source of U and the drain of U, V, and P.)
The fact that all the interactions are local makes this a good
candidate for a parallel implementation. Diffusion may be modeled by
an explicitly conservative exchange process among neighbors where
the reactions are locally modeled at each locus by a simulated processor.
|
Xmorphia shows a
beautiful presentation of a simulation of the Gray-Scott reaction
diffusion mechanism using a uniform-grid finite-difference model
running on an Intel Paragon supercomputer. We are interested in
being able to make such simulations with an amorphous computer where
the precise positions of the individual processing elements is uncertain.
The physical world appears to be homogeneous and isotropic at the
scale of atoms and molecules, so the precise positions of the reaction
sites should not be essential to the character of the patterns
produced by the chemistry. We can test this by comparing a simulation
of similar situations using a crystalline array or an amorphous
computer. The simulator presented here allows us to conveniently make
this comparison.
You can run a Java version of our simulator to see for yourself how the patterns are formed
The following figures, made with a simulator written in
Scheme,
illustrate the kind of patterns that can be obtained by varying the
grid.
In these simulations each locus of
reaction is represented by a simulated processor. The processors are
asychronous: each one runs its simulation steps at randomly chosen
times. Each simulation step is stoichiometrically conservative.
In each of these figures we have 4000 loci of reaction. The
parameters are: f = 0.04, k = 0.06, r_u = 0.01, r_v = 0.005. The
neighborhood radius is 0.04. (So each simulated processor has
approximately 20 neighbors.)
The colors show the concentration of U at each locus. Red labels the
maximum concentration and Blue labels the minimum concentration. The
patterns that you see are stable -- no significant change will occur,
regardless of how long we run the process. Each pattern starts off
from the same slightly randomized initial condition. The differences
among the patterns is due to either the differences of the grids or
the differences in the initial condition.

Amorphous layout (random, smoothed)

Hexagonal close packed layout
|

Square layout

Another Amorphous layout
|
Although the details differ, we can see that the general character of
the patterns developed are similar, independent of the grid. The
features have similar sizes and shapes. They are somewhat aligned
with the boundaries.
If we decrease the radius of the neighborhood to 0.03, thereby
decreasing the average number of neighbors to about 11
(4000*3.14*0.03*0.03), we get correspondingly more delicate features.

Amorphous layout (random, smoothed)
|

Hexagonal close packed layout
|
Interestingly, as the amorphous layout shows, the alignment of the
features with the boundary is less sure as the features become small
by comparison to the figure.
If you have a fast network connection, you can view some MPEG movies
we've made with the asychronous Scheme simulator that show how the
process evolves. The first three movies show evolution with the same
set of parameters, f = 0.025, k = 0.06, r_u = 0.01, r_v = 0.005. In
each movie the reaction occurs at 4000 sites with a neighborhood
radius of 0.04. The entire image is of unit size in both the
horizontal and vertical direction. In these movies the reaction is
occuring asynchronously in that at each instant a random site is
activated to do one conservative reaction step. We consider 4000 such
individual reaction steps (one for each locus) to be "equivalent" to
one full step of a synchronous simulation. Each movie spans 6400 full
steps. The movie is made by making frames that periodically sample at
integral numbers of full steps.
What is important to notice here is how the qualitative nature of the
evolution is independent of the layout of the loci of reaction, and
also that the use of asynchronous update produces similar results to
those produced by the synchronous simulation performed by the Java
simulator we provide, and by the traditional finite-difference results
of Xmorphia.
The first movie shows the
evolution on an amorphous layout. This movie's frames are taken at 16-step
intervals.
The second movie shows the same
parameters running on a hexagonal grid. This movie's frames are taken at 16-step
intervals.
The third movie shows them running on
a square grid, but this time each frame is taken at 8-step intervals,
so the picture evolves more slowly.
Our fourth movie shows a different set
of parameters, f = 0.024, k = 0.055, r_u = 0.01, r_v = 0.005. Like
the first movie, this is running on
an amorphous layout of 4000 loci, neighborhood radius 0.04, 16 steps
per frame.
The following movies were made using the Java synchronous simulator .
Like the asynchronous Scheme
simulations above, there were 4000 loci, the neighborhood radius was
0.04, and the processors were placed randomly in the unit square.
Frames in each movie were taken at 10 step intervals, and each
simulation was allowed to run for at least 5400 steps. The diffusion
parameters and the time step were kept constant at r_u = 0.01, r_v =
0.005 and dt = 1.0 for each simulation.
-
This simulation provides a basis for comparison between the two
simulators. Notice that the stationary patterns formed by the two
simulators are qualitatively similar even though the Java simulator
updates synchronously while the other does not.
-
The pattern formed in this simulation is reminiscent of a leopard's
skin. The manner in which the "spots" form is interesting in itself
because the process closely resembles cell division.
The following two simulations demonstrate dynamic patterns. That is,
no stationary pattern forms within any reasonable amount of time
(simulation 4 was run for over 800,000 steps, and there was no visible
sign of any less activity than there was at say 4000 steps). These
were included to show that the amorphous simulations can qualitatively
capture both the static and dynamic patterns described in Pearson's
article.
-
This pattern is probably best described as "wandering bubbles."
The bubbles repeatedly collide with and annihilate each other, only
to be regenerated from the residual patterns of those collisions.
-
This pattern is characterized by colliding "waves" of color. Large
contiguous sections of the field will assume a single color, only to
be quickly displaced by the insurgence of another color, that usually
originates from an edge or corner of the field.
Belorussian
translation