Meeting 8: Lifting Transformations, Geometric Reductions

Announcement:  Felice Frankel speaks at 4pm in 34-101 !

Introductory Remarks:

This course is about tools and tool-building.  One issue that comes up
frequently in geometric computation is this:  when faced with a new
problem, can an existing tool be re-used, or must a new tool always
be built from scratch?

Today, we will discuss methods for transforming new problems into
problems that we know how to solve.  There are two parts to this:
finding a useful relationship between problem statements, and
devising efficient algorithms to transform between them.  We'll
cover these in opposite order.

This effectively expands our repertoire of tools, without a lot of extra work.

Presenters:

Jon Heiner

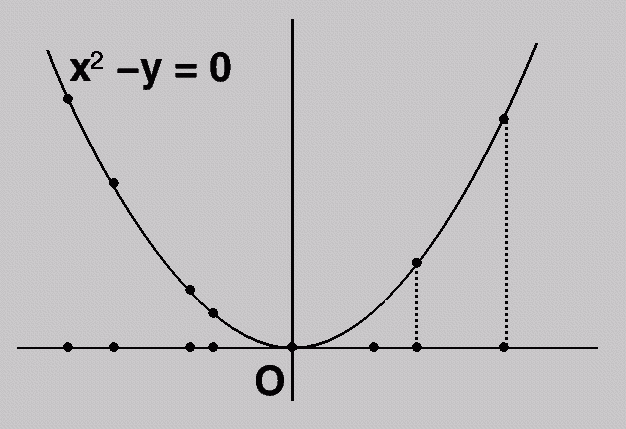
A Lifting transformation:  d-dimensional voronoi diagrams
to (d+1)-dimensional convex (lower) hulls.
 

Wish to compute a Voronoi diagram in d dimensions.  Input
is n points.  Example:  d == 1 (shown).

We will show (from P&S Section 6.3) a lifting transformation
that maps d-dim Voronoi Diagrams to (d+1)-dim lower hulls.

First, lift the real line (and thus the set of sites) onto a parabola
as shown above.

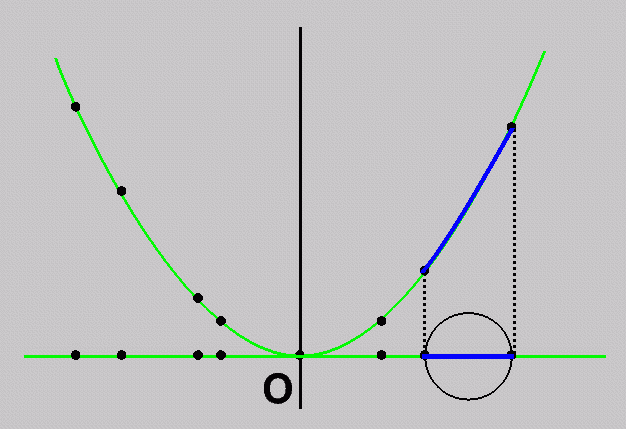
Notice the destination of:
    the real line (green)
    the discrete sites (black)
    the portion of the line between two sites (blue)
        (what is the black circle?)
 

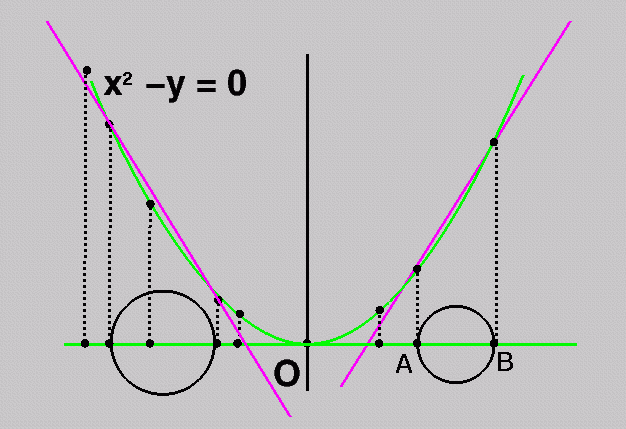
Now for any two sites, construct the chord through their lifted
positions (magenta).

This chord meets the parabola in exactly two points (why?).
Thus is partitions the parabola into an interior and exterior
portion -- exactly the lifting of the portion of the line between
the generating sites.  Notice that these portions lie on opposite
sides of the chord in the plane.

Now look at the chord and its relation to the other (n-2) lifted
sites.  When will the chord support an edge of the lower hull
of the lifted sites?

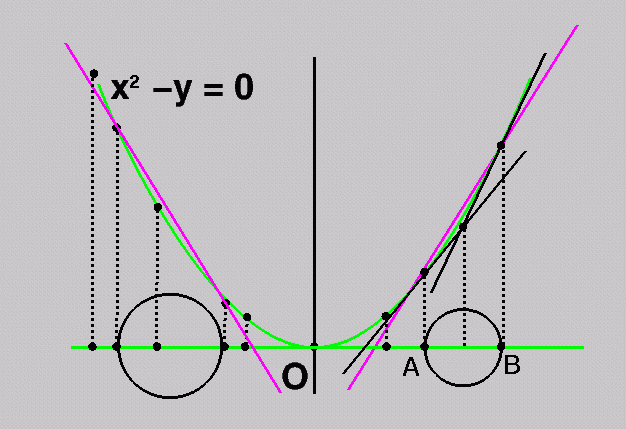
The only way for a lifted site C to lie "outside" the chord is
if the generator (unlifted) site lay "inside" the circumcircle
of the generator sites A and B.

Thus the structure of a Voronoi diagram of n sites in d
dimensions -- that is, a set of empty circles centered on
Voronoi vertices, each passing through d sites, is exactly
that of the convex hull of the same n sites lifted onto a
paraboloid in (d+1) dimensions.

More neat things:  this works in any dimension (show d=2,3),
and it works for an arbitrarily translated paraboloid!

Readings:

• de Berg Chapter 8
• Preparata and Shamos Section 6.3

• idual
• voronoi

Next Meeting

Last Meeting .... Next Meeting .... Course Page .... Meeting Schedule

Created: Feb 1998